转载：SVD

ComputeSVD

        在分布式矩阵有CoordinateMatirx,
RowMatrix, IndexedRowMatrix三种。除了CoordinateMatrix之外,IndexedRowMatrix和RowMatrix都有computeSVD方法，并且CoordinateMatrix有toIndexedRowMatrix()方法和toRowMatrix()方法可以向IndexedRowMatrix

和RowMatrix两种矩阵类型转换。

   

因此主要对比

IndexedRowMatrix

和

RowMatrix

两种矩阵类型的

ComputSVD

算法进行分析
   关于SVD内容请参看维基百科，和一篇很棒的博文：《机器学习中的数学》进行了解。

一 算法描述：

           def   computeSVD

( k: Int, computeU: Boolean = false, rCond: Double = 1e-9):

         
                       
IndexedRowMatrix 

返回类型： 
SingularValueDecomposition[IndexedRowMatrix, Matrix]
                       
RowMatrix              

返回类型： 
SingularValueDecomposition[RowMatrix, Matrix] 



                 U                is a RowMatrix of size m x k that satisfies U' * U = eye(k),

                 S                  is a Vector of size k, holding the singular values in descending order,

                 V                  is a Matrix of size n x k that satisfies V' * V = eye(k).



               k 
               number of leading singular values to keep (0 < k <= n). It might return less than k if there are 
                                    numerically zero singular values or there are not enough Ritz values converged before the 
                                    maximum number of Arnoldi update iterations is reached.


                 computeU   whether to compute U

                 rCoud         the reciprocal condition number. All singular values smaller than rCond * sigma(0) are treated as zero, 
                                    where sigma(0) is the largest singular value.

                 return         SingularValueDecomposition(U, s, V). U = null if computeU = false. 



二 选择例子：

构建一个4×5的矩阵M:

      

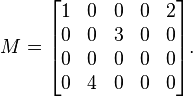
矩阵的形式为svdM.txt :

                        1  0  0  0  2
                        0  0  3  0  0
                        0  0  0  0  0
                        0  4  0  0  0

M矩阵的奇异值分解后奇异矩阵s应为：

               4  0  0  0  0
                           0  3  0  0  0
                           0  0 √5 0  0
                           0  0  0  0  0

我们将通过ComputeSVD函数进行验证.

三 构造矩阵,运行算法并验证结果：   

<一> 构造RowMatrix矩阵:M
 
        scala> val M = new RowMatrix(sc.textFile("hdfs:///usr/matrix/svdM.txt").map(_.split(' '))
                                                 .map(_.map(_.toDouble)).map(_.toArray)
                                                 .map(line => Vectors.dense(line)))
        M: org.apache.spark.mllib.linalg.distributed.RowMatrix = org.apache.spark.mllib.linalg.distributed.RowMatrix

<二> 调用算法
         scala> val svd = M.computeSVD(4, true)
         svd: SingularValueDecomposition[RowMatrix,Matrix]
         可以看到svd是一个SingularValueDecomposition类型的对像，内部包含一个RowMatrix和一个Matrix用算法,并且此处的RowMatrix就是左奇异向量U，Matrix就是右奇异向量V.

<三> 验证结果

SingularValueDecomposition类API如下：
        

矩阵M的左奇异向量U：
        scala> scala> val U = svd.U
                   U: org.apache.spark.mllib.linalg.distributed.RowMatrix = org.apache.spark.mllib.linalg.distributed.RowMatrix
         scala> U.rows.foreach(println)
                    [0.0 ,0.0 ,  -0.9999999999999999 ,  -1.4901161193847656E-8]
                    [0.0 ,1.0 ,0.0 ,0.0]
                    [0.0 ,0.0 ,0.0 ,0.0]
                   [-1.0 ,0.0 ,0.0 ,0.0]

矩阵M的奇异值s：
         scala> val s = svd.s
                   s:  org.apache.spark.mllib.linalg.Vector = [4.0,3.0,2.23606797749979,1.4092648163485167E-8]

矩阵M的右奇异向量V：
         scala> val V = svd.V
                    V: org.apache.spark.mllib.linalg.Matrix =
                    0.0    0.0    -0.44721359549995787     0.8944271909999159
                    -1.0   0.0    0.0    0.0
                    0.0    1.0    0.0    0.0
                    0.0    0.0    0.0    0.0
                    0.0    0.0   -0.8944271909999159       -0.447213595499958