哈喽，好久没来了，最近搞自动化发现了很多代码弯路，特别分享出来给能用到的朋友

因为公司业务的关系，每做一笔功能冒烟测试，我们就要对很多的数据库表中的字段进行校验，当时我就想反正总是要重复的运行这些SQL语句，

干脆就把这些SQL语句写到一个py文件里，需要执行相应的SQL语句就去进行调用，刚开始感觉没什么问题，在testcase里边感觉调用起来很方便，

当时py文件里边写SQL语句就是如下的状态：

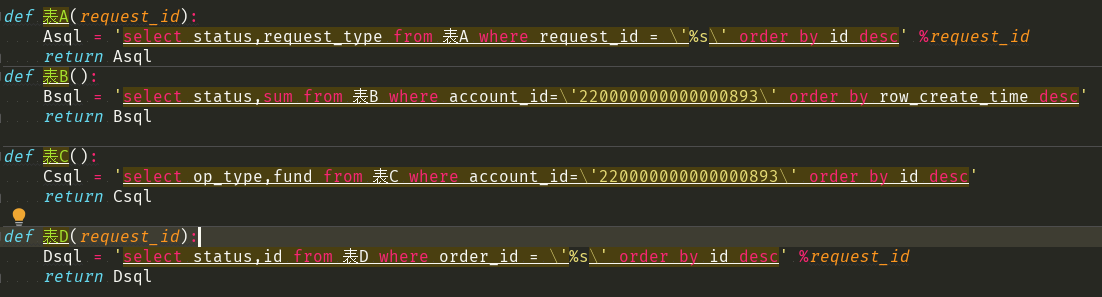
当时的心情，开心的溢于言表，然后其他同事也一起将检查表的SQL语句加入到了这个py文件里

可是随着业务模块的增加，检查的表格过多需要执行的SQL语句也越来越多，整个py文件看起来过于臃肿，对于case运行起来的效率也慢了很多

后来就上网查询了一下，干脆写一个实用的方法来代替写这些SQL语句，方法的参数分为三个部分，表名-查询字段（list）-条件

写完的方法如下如：

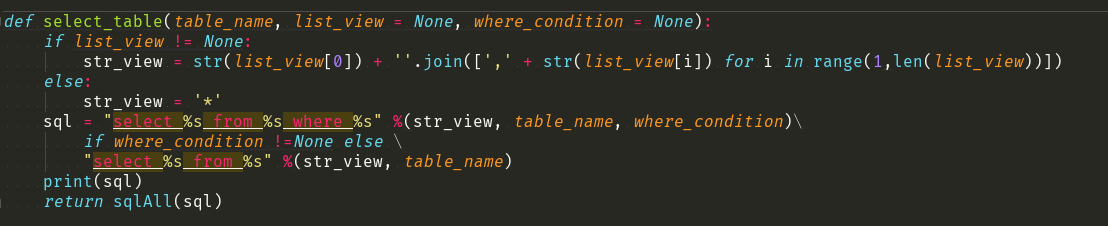
这样就将不可计数的SQL语句写成一个方法代替，大大提升了代码的可读性，如果有需要的朋友可以这样去进行使用，欢迎阅读，谢谢！！！

用python实现数据库查询数据方法的更多相关文章

  1. 用struts2标签如何从数据库获取数据并在查询页面显示。最近做一个小项目，需要用到struts2标签从数据库查询数据，并且用迭代器iterator标签在查询页面显示，可是一开始，怎么也获取不到数据，想了许久，最后发现，是自己少定义了一个变量，也就是var变量。

    最近做一个小项目,需要用到struts2标签从数据库查询数据,并且用迭代器iterator标签在查询页面显示,可是一开始,怎么也获取不到数据,想了许久,最后发现,是自己少定义了一个变量,也就是var变 ...

  2. ORACLE跨数据库查询的方法

    原文地址:http://blog.csdn.net/huzhenwei/article/details/2533869 本文简述了通过创建database link实现Oracle跨数据库查询的方法 ...

  3. C#连接Oracle数据库查询数据

    C#连接Oracle数据库可以实现许多我们需要的功能,下面介绍的是C#连接Oracle数据库查询数据的方法,如果您对C#连接Oracle数据库方面感兴趣的话,不妨一看. using System; u ...

  4. mongodb基础系列——数据库查询数据返回前台JSP（二）

    上篇博客论述了,数据库查询数据返回前台JSP.博客中主要使用Ajax调用来显示JSON串,来获取其中某一个字段,赋给界面中的某一个控件. 那这篇博客中,我们讲解,把后台List传递JSP展示. Lis ...

  5. SpringMVC——项目启动时从数据库查询数据

    SpringMVC项目中遇到这样的问题: 1.很多数据字典需要从数据库中查询: 2.懒得修改SQL语句: 3.想在项目中声明静态变量存储数据字典,但是希望这个字典可以在项目启动时进行加载. 当遇到这样 ...

  6. MySQL 数据库查询数据，过滤重复数据保留一条数据---（MySQL中的row_number变相实现方法）

    转自: http://www.maomao365.com/?p=10564 摘要: 下文讲述MySQL数据库查询重复数据时,只保留一条数据的方法 实现思路: 在MySQL数据库中没有row_numbe ...

  7. python自动化测试之mysql5.0版本数据库查询数据时出现乱码问题分析

    1.确保数据库编码是utf8编码.若不是,请将my.ini的client,mysql,mysqld三个字段下面添加default-character-set = utf8,这样可以永久改变在新建数据库 ...

  8. 使用Connector / Python连接MySQL/查询数据

    使用Connector / Python连接MySQL connect()构造函数创建到MySQL服务器的连接并返回一个 MySQLConnection对象 在python中有以下几种方法可以连接到M ...

  9. mongodb基础系列——数据库查询数据返回前台JSP（一）

    经过一段时间停顿,终于提笔来重新整理mongodb基础系列博客了. 同时也很抱歉,由于各种原因,没有及时整理出,今天做了一个demo,来演示,mongodb数据库查询的数据在JSP显示问题. 做了一个 ...

随机推荐

  1. spring cloud Eureka server 问题 Spring Cloud java.lang.TypeNotPresentException

    版本: spring-cloud.version : Greenwich.SR2 pom配置: <project xmlns="http://maven.apache.org/POM/ ...

  2. Logstash配置同步mysql到es配置

    关于logstash安装:https://www.cnblogs.com/toov5/p/10301727.html Logstash是一个开源数据收集引擎,具有实时管道功能.Logstash可以动态 ...

  3. Pytest单元测试框架-Pytest环境安装

    unittest是python自带的单元测试框架,它封装好了一些校验返回的结果方法和一些用例执行前的初始化操作,使得单元测试易于开展,因为它的易用性,很多同学也拿它来做功能测试和接口测试,只需简单开发 ...

  4. [LeetCode] 114. Flatten Binary Tree to Linked List 将二叉树展平为链表

    Given a binary tree, flatten it to a linked list in-place. For example, given the following tree: 1 ...

  5. 禅道的使用—bug管理工具

    简介 禅道项目管理软件集产品管理.项目管理.质量管理.文档管理.组织管理和事务管理于一体,是一款功能完备的项目管理软件,完美地覆盖了项目管理的核心流程. 1.禅道使用的基本流程 禅道管理软件中,核心的 ...

  6. laravel Carbon函数

    原文地址:https://blog.csdn.net/lbwo001/article/details/53063867 carbon官方网站:https://carbon.nesbot.com/doc ...

  7. mybatis中封装结果集常见示例

    1.返回一个对象 public interface EmployeeMapper { public Employee getEmpByMap(Map<String, Object> map ...

  8. Prometheus入门到放弃(7)之redis_exporter部署

    redis监控,prometheus需要使用redis_exporter客户端. 这里我们采用docker方式部署,既可以部署在redis所在服务器,也可以部署在其他机器: docker镜像地址:ht ...

  9. CSP前的板子们

    见窝的luogu博客qwq noip前的板子们

  10. 【LEETCODE】47、985. Sum of Even Numbers After Queries

    package y2019.Algorithm.array; /** * @ProjectName: cutter-point * @Package: y2019.Algorithm.array * ...