网络流之最大流Dinic --- poj 1459
Description
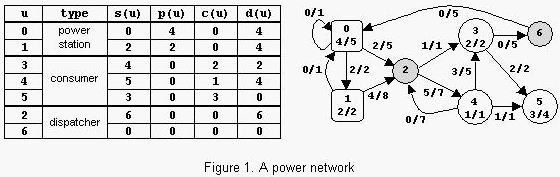
Input
Output
Sample Input
2 1 1 2 (0,1)20 (1,0)10 (0)15 (1)20
7 2 3 13 (0,0)1 (0,1)2 (0,2)5 (1,0)1 (1,2)8 (2,3)1 (2,4)7
(3,5)2 (3,6)5 (4,2)7 (4,3)5 (4,5)1 (6,0)5
(0)5 (1)2 (3)2 (4)1 (5)4
Sample Output
15
6
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <queue>
using namespace std;
const int N = ;
const int MAXN = 1e9 + ; struct Edge {
int to;
int value;
int next;
}e[*N*N];
int head[N], cnt;
int deep[N];
int n, np, nc, m; void insert(int u, int v, int value) {
e[++cnt].to = v;
e[cnt].value = value;
e[cnt].next = head[u];
head[u] = cnt;
} void init() {
memset(head, -, sizeof(head));
cnt = -;
} bool BFS() {
memset(deep,-,sizeof(deep));
queue<int> Q;
deep[] = ;
Q.push();
while (!Q.empty()) {
int u = Q.front();
Q.pop();
for (int edge = head[u]; edge != -; edge = e[edge].next) {
int v = e[edge].to;
if (deep[v] == - && e[edge].value > ) {
deep[v] = deep[u] + ;
Q.push(v);
}
}
}
if (deep[n + ] == -) return false;
return true;
} int DFS(int u,int flow_pre) {
if (u == n + ) return flow_pre;
int flow = ;
for (int edge = head[u]; edge != -; edge = e[edge].next) {
int v = e[edge].to;
if (deep[v] != deep[u]+ || e[edge].value==) continue;
int _flow= DFS(v, min(flow_pre, e[edge].value));
flow_pre -= _flow;
flow += _flow;
e[edge].value -= _flow;
e[edge ^ ].value += _flow;
if (flow_pre == ) break;
}
if (flow == ) deep[u] = -;
return flow;
}
int GetMaxFlow() {
int ans = ;
while (BFS()) {
ans += DFS(,MAXN);
}
return ans;
}
int main()
{
while (scanf("%d%d%d%d", &n, &np, &nc, &m) != EOF) {
init();
int u, v, z;
for (int i = ; i < m; i++) {
scanf(" (%d,%d)%d", &u, &v, &z);
insert(u+, v+, z);
insert(v+, u+, );
}
for (int i = ; i < np; i++) {
scanf(" (%d)%d", &u, &z);
insert(, u+, z);
insert(u+, , );
}
for (int i = ; i < nc; i++) {
scanf(" (%d)%d", &u, &z);
insert(u + , n + , z);
insert(n + , u + , );
}
printf("%d\n",GetMaxFlow());
}
}
网络流之最大流Dinic --- poj 1459的更多相关文章
- 网络流之最大流EK --- poj 1459
题目链接 本篇博客延续上篇博客(最大流Dinic算法)的内容,此次使用EK算法解决最大流问题. EK算法思想:在图中搜索一条从源点到汇点的扩展路,需要记录这条路径,将这条路径的最大可行流量 liu 增 ...
- 网络流之最大流Dinic算法模版
/* 网络流之最大流Dinic算法模版 */ #include <cstring> #include <cstdio> #include <queue> using ...
- 我爱网络流之最大流Dinic
直接上大佬博客: Dinic算法详解及实现来自小菲进修中 Dinic算法(研究总结,网络流)来自SYCstudio 模板步骤: 第一步,先bfs把图划分成分成分层图网络 第二步,dfs多次找增广路 当 ...
- 网络流(最大流-Dinic算法)
摘自https://www.cnblogs.com/SYCstudio/p/7260613.html 网络流定义 在图论中,网络流(Network flow)是指在一个每条边都有容量(Capacity ...
- [Poj2112][USACO2003 US OPEN] Optimal Milking [网络流,最大流][Dinic+当前弧优化]
题意:有K个挤奶机编号1~K,有C只奶牛编号(K+1)~(C+K),每个挤奶机之多能挤M头牛,现在让奶牛走到挤奶机处,求奶牛所走的最长的一条边至少是多少. 题解:从起点向挤奶机连边,容量为M,从挤奶机 ...
- POJ 1459 Power Network / HIT 1228 Power Network / UVAlive 2760 Power Network / ZOJ 1734 Power Network / FZU 1161 (网络流,最大流)
POJ 1459 Power Network / HIT 1228 Power Network / UVAlive 2760 Power Network / ZOJ 1734 Power Networ ...
- POJ 2711 Leapin' Lizards / HDU 2732 Leapin' Lizards / BZOJ 1066 [SCOI2007]蜥蜴(网络流,最大流)
POJ 2711 Leapin' Lizards / HDU 2732 Leapin' Lizards / BZOJ 1066 [SCOI2007]蜥蜴(网络流,最大流) Description Yo ...
- POJ 3436 ACM Computer Factory (网络流,最大流)
POJ 3436 ACM Computer Factory (网络流,最大流) Description As you know, all the computers used for ACM cont ...
- poj 1459 多源多汇点最大流
Sample Input 2 1 1 2 (0,1)20 (1,0)10 (0)15 (1)20 7 2 3 13 (0,0)1 (0,1)2 (0,2)5 (1,0)1 (1,2)8 (2,3)1 ...
随机推荐
- python的gRPC示例
参考URL: https://segmentfault.com/a/1190000015220713?utm_source=channel-hottest gRPC 是一个高性能.开源和通用的 RPC ...
- Rest微服务案例(二)
1. 创建父工程 Maven Project 新建父工程microservicecloud,packaging是pom模式,pom.xml内容如下: <!-- SpringBoot父依赖 --& ...
- luoguP4103 [HEOI2014]大工程
题意 建出虚树DP. 设\(f[i]\)表示i的子树的第一问答案,\(minn[i]\)表示\(i\)的子树中到\(i\)最近的关键点,\(maxx[i]\)表示\(i\)的子树中到i距离最远的关键点 ...
- table的常用属性
Table属性: Cellspacing:单元格与单元格之间或者单元格与表格之间的 距离. Cellpadding:单元格边框与内容之间的距离 Colspan:跨列.合并列. Rowspan:跨行,行 ...
- 2019 SDN阅读作业(2)
1.过去20年中可编程网络的发展可以分为几个阶段?每个阶段的贡献是什么? 可编程网络的发展可以分为以下三个阶段: (1)主动网络(Active networking,20世纪90年代中期到21世纪初) ...
- 【CometOJ】Comet OJ - Contest #8 解题报告
点此进入比赛 \(A\):杀手皇后(点此看题面) 大致题意: 求字典序最小的字符串. 一场比赛总有送分题... #include<bits/stdc++.h> #define Tp tem ...
- Asp.Net Core 工作单元 UnitOfWork UOW
Asp.Net Core 工作单元示例 来自 ABP UOW 去除所有无用特性 代码下载 : 去除所有无用特性版本,原生AspNetCore实现 差不多 2278 行代码: 链接:https://pa ...
- 强大的性能监测工具dstat
强大的性能监测工具dstat 本节分为以下几个部分: dstat介绍: dstat命令是一个用来替换vmstat.iostat.netstat.nfsstat和ifstat这些命令的工具,是一个全能系 ...
- python asyncio asyncio wait
import asyncio import time async def get_html(url): print("start get url") await asyncio.s ...
- 初探云原生应用管理(一): Helm 与 App Hub
系列介绍:初探云原生应用管理系列是介绍如何用云原生技术来构建.测试.部署.和管理应用的内容专辑.做这个系列的初衷是为了推广云原生应用管理的最佳实践,以及传播开源标准和知识.通过这个系列,希望帮 ...
