hdu 1828 线段树扫描线(周长)

Picture

Time Limit: 6000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3897    Accepted Submission(s): 1978

Problem Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

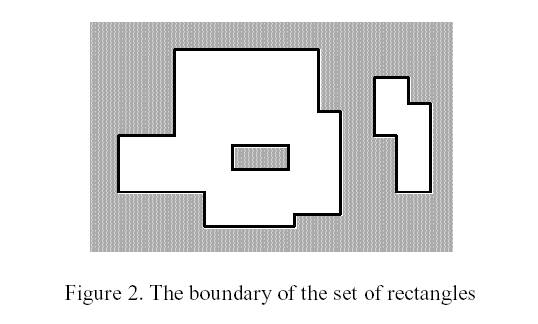
The vertices of all rectangles have integer coordinates.

 

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.

0 <= number of rectangles < 5000 
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Please process to the end of file.

 

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

 

Sample Input

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

Sample Output

228

First

/*
hdu 1828 线段树扫描线(周长)
 
给你一些矩阵,有部分or全部重叠.求最终图形的周长
 
对于x轴的边,矩阵的下边标为1,矩阵的上边标为-1.每次插入后用当前覆盖面积
减去上一次的覆盖面积(即新增长度)，扫描过一个矩阵的上边后便能消除下边的
影响。
对x,y轴分别扫描一次即可
 
最开始没考虑重边的问题,结果C++ AC(G++ WR)
然后更改后G++才过 - -
 
2
0 0 1 1
1 0 2 1
 
2
0 0 1 1
0 1 1 2
 
hhh-2016-03-26 16:35:21
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <functional>
using namespace std;
#define lson  (i<<1)
#define rson  ((i<<1)|1)
typedef long long ll;
const int maxn = 20050;
int a[maxn];
struct node
{
    int l,r;
    int sum,len;
    int mid()
    {
        return (l+r)>>1;
    }
} tree[maxn*5];
 
void push_up(int i)
{
    if(tree[i].sum)
        tree[i].len = (tree[i].r-tree[i].l+1);
    else if(tree[i].l == tree[i].r)
        tree[i].len = 0;
    else
        tree[i].len = tree[lson].len+tree[rson].len;
}
 
void build(int i,int l,int r)
{
    tree[i].l = l;
    tree[i].r = r;
    tree[i].sum = 0;
    tree[i].len = 0;
    if(l == r)
        return ;
 
    int mid = tree[i].mid();
    build(lson,l,mid);
    build(rson,mid+1,r);
    push_up(i);
}
 
void push_down(int i)
{
//    if(tree[i].sum)
//    {
//        tree[lson].sum += tree[i].sum;
//        tree[rson].sum += tree[i].sum;
//        tree[lson].len = tree[lson].r-tree[lson].l;
//        tree[rson].len = tree[rson].r-tree[rson].l;
//    }
}
 
void Insert(int i,int l,int r,int val)
{
    if(tree[i].l >= l && tree[i].r <=r )
    {
        tree[i].sum += val;
        push_up(i);
        return ;
    }
    int mid = tree[i].mid();
    push_down(i);
    if(l <= mid)
        Insert(lson,l,r,val);
    if(r > mid)
        Insert(rson,l,r,val);
    push_up(i);
}
 
struct edge
{
    int l,r;
    int va,high;
};
edge tx[maxn*2];
edge ty[maxn*2];
 
bool cmp(edge a,edge b)
{
    if(a.high != b.high)
        return a.high < b.high;
    else   //如果有重边则要先插入在删除
        return a.va > b.va;
}
 
int main()
{
    int n;
    while(scanf("%d",&n) != EOF)
    {
        int x1,x2,y1,y2;
        int tox = 0,lx=0x3f3f3f3f,rx=0;
        int toy = 0,ly=0x3f3f3f3f,ry=0;
        for(int i = 1; i <= n; i++)
        {
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
            lx = min(x1,lx),rx = max(rx,x2);
            ly = min(y1,ly),ry = max(ry,y2);
            tx[tox].l = x1,tx[tox].r = x2,tx[tox].high=y1,tx[tox++].va=1;
            tx[tox].l = x1,tx[tox].r = x2,tx[tox].high=y2,tx[tox++].va=-1;
            ty[toy].l = y1,ty[toy].r = y2,ty[toy].high=x1,ty[toy++].va=1;
            ty[toy].l = y1,ty[toy].r = y2,ty[toy].high=x2,ty[toy++].va=-1;
        }
        sort(tx,tx+tox,cmp);
        sort(ty,ty+toy,cmp);
        int ans=0,prelen = 0;
        build(1,lx,rx-1);
        for(int i = 0; i < tox; i++)
        {
            Insert(1,tx[i].l,tx[i].r-1,tx[i].va);
            ans += abs(tree[1].len-prelen);
            prelen = tree[1].len;
        }
        //cout << ans <<endl;
        build(1,ly,ry-1);
        prelen = 0;
        for(int i = 0; i < toy; i++)
        {
            Insert(1,ty[i].l,ty[i].r-1,ty[i].va);
            ans += abs(tree[1].len-prelen);
            prelen = tree[1].len;
        }
        cout << ans <<endl;
    }
    return 0;
}

　　

Second

/*
hdu 1828 线段树扫描(周长)2
 
在向上扫描的过程中我们可以计算出平行于x轴的长度
然后在两条线之间我们只需要计算出有多少条竖线便能得带这两条线之间平行于
y轴的长度。
用ls和rs来表示当前节点左右端点是否被覆盖
在处理竖线数量时,注意合并带来的影响,假设lson.rs和rson.ls都存在值的话
说明存在重叠的部分
 
hhh-2016-03-26 17:58:50
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <functional>
using namespace std;
#define lson  (i<<1)
#define rson  ((i<<1)|1)
typedef long long ll;
const int maxn = 20050;
int a[maxn];
struct node
{
    int l,r;
    int sum,len;
    int num,ls,rs;
    int mid()
    {
        return (l+r)>>1;
    }
} tree[maxn*5];
 
void push_up(int i)
{
    if(tree[i].sum)
    {
        tree[i].len = (tree[i].r-tree[i].l+1);
        tree[i].ls = tree[i].rs = 1;
        tree[i].num = 1;
    }
    else if(tree[i].l == tree[i].r)
    {
        tree[i].len= 0;
        tree[i].num=tree[i].rs=tree[i].ls=0;
    }
    else
    {
        tree[i].len = tree[lson].len+tree[rson].len;
        tree[i].ls = tree[lson].ls;
        tree[i].rs = tree[rson].rs;
        tree[i].num = tree[lson].num+tree[rson].num;
        tree[i].num -= (tree[lson].rs&tree[rson].ls);
        //减去重叠的部分
    }
}
 
void build(int i,int l,int r)
{
    tree[i].l = l;
    tree[i].r = r;
    tree[i].sum = tree[i].len = 0;
    tree[i].ls = tree[i].rs = tree[i].num = 0;
    if(l == r)
        return ;
 
    int mid = tree[i].mid();
    build(lson,l,mid);
    build(rson,mid+1,r);
    push_up(i);
}
 
void push_down(int i)
{
 
}
 
void Insert(int i,int l,int r,int val)
{
    if(tree[i].l >= l && tree[i].r <=r )
    {
        tree[i].sum += val;
        push_up(i);
        return ;
    }
    int mid = tree[i].mid();
    push_down(i);
    if(l <= mid)
        Insert(lson,l,r,val);
    if(r > mid)
        Insert(rson,l,r,val);
    push_up(i);
}
 
struct edge
{
    int l,r;
    int va,high,id;
};
edge tx[maxn*2];
 
bool cmp(edge a,edge b)
{
    if(a.high != b.high)
        return a.high < b.high;
    else
        return a.va > b.va;
}
 
int main()
{
    int n;
    while(scanf("%d",&n) != EOF)
    {
        int x1,x2,y1,y2;
        int tox = 0,lx=0x3f3f3f3f,rx=0;
        for(int i = 1; i <= n; i++)
        {
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
            lx = min(x1,lx),rx = max(rx,x2);
            tx[tox].l = x1,tx[tox].r = x2,tx[tox].high=y1,tx[tox++].va=1;
            tx[tox].l = x1,tx[tox].r = x2,tx[tox].high=y2,tx[tox++].va=-1;
        }
        sort(tx,tx+tox,cmp);
        int ans=0,prelen = 0;
        build(1,lx,rx-1);
        //tx[tox] = tx[tox+1];
        for(int i = 0; i < tox; i++)
        {
            Insert(1,tx[i].l,tx[i].r-1,tx[i].va);
            ans += abs(tree[1].len-prelen);
            if(i != tox-1)
            ans += (tx[i+1].high-tx[i].high)*tree[1].num*2;
            prelen = tree[1].len;
        }
        cout << ans <<endl;
    }
    return 0;
}