poj 1704 Georgia and Bob(阶梯博弈)

Georgia and Bob

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 9363		Accepted: 3055

Description

Georgia and Bob decide to play a self-invented game. They draw a row of grids on paper, number the grids from left to right by 1, 2, 3, ..., and place N chessmen on different grids, as shown in the following figure for example: 

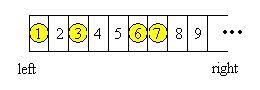
Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game.

Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out.

Given the initial positions of the n chessmen, can you predict who will finally win the game?

Input

The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case contains two lines. The first line consists of one integer N (1 <= N <= 1000), indicating the number of chessmen. The second line contains N different integers P1, P2 ... Pn (1 <= Pi <= 10000), which are the initial positions of the n chessmen.

Output

For each test case, prints a single line, "Georgia will win", if Georgia will win the game; "Bob will win", if Bob will win the game; otherwise 'Not sure'.

Sample Input

2
3
1 2 3
8
1 5 6 7 9 12 14 17

Sample Output

Bob will win
Georgia will win

/*
poj 1704 Georgia and Bob(阶梯博弈)

一行棋盘，每次可以将一个棋子往左边移动，但是不能跨越棋子
每次移动时，和左边的间距变小了，与右边的间距变大
可以等效于阶梯博弈，每次将一个台阶上的棋子往下移动。 本台阶石子变少，下一个台阶的石子边多
转化一下就好了

hhh-2016-08-02 21:26:32
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <functional>
typedef long long ll;
#define lson (i<<1)
#define rson ((i<<1)|1)
using namespace std;
const int maxn = 10000+10;

int sg[maxn];
int s[maxn];
int n;

void SG(int now)
{
    if(sg[now] != -1)
        return ;
    int vis[maxn];
    memset(vis,0,sizeof(vis));
    for(int i = 0; i < n; i++)
    {
        int t = now-s[i];
        if(t < 0)
            continue;
        SG(t);
        vis[sg[t]] = 1;
    }

    for(int i = 0;; i++)
    {
        if(!vis[i])
        {
            sg[now] = i;
            break;
        }
    }
}

int main()
{
    int x,m;
    int a[maxn];
//    freopen("in.txt","r",stdin);
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n) ;
        for(int i = 0; i < n; i++)
        {
            scanf("%d",&a[i]);
        }
        sort(a,a+n);
        int ans;
        if(n % 2 == 0)
        ans = 0;
        else
            ans = a[0]-1;
        for(int i = n-1; i > 0; i -= 2)
        {
            ans ^= (a[i] - a[i-1] -1);
        }
        if(ans)
            printf("Georgia will win\n");
        else
            printf("Bob will win\n");
    }
    return 0;
}