C语言实现快速排序法（分治法）

---

title: 快速排序法（quick sort）

tags: 分治法（divide and conquer method）

grammar_cjkRuby: true

算法原理

分治法的基本思想：将原问题分解为若干个更小的与原问题相似的问题，然后递归解决各个子问题，最后再将各个子问题的解组合成原问题的解。

利用分治法可以将解决办法分为 “三步走” 战略：

（1） 在数据集中选定一个元素作为“基准”（pivot）

（2） 将所有数据集小于基准的元素放在基准左边，大于基准的元素放在基准右边，把原数据集分为两个数据集的操作叫做“分区”，分区结束后基准所在的位置也就是基准最后的位置

（3） 分别对基准左右两边的数据集进行前两个步骤，直至数据集只剩下一个数据为止

C语言实现

/***********************/
//章节：第四章
//内容：快速排序
/***********************/
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<sys/stat.h>

void fastsort(int v[], int first, int last); 

int main()
{
	int i, v[10] = {1,243,43,5,6,634,434,23,12,7};
	fastsort( v, 0, 9);
	for(i = 0; i < 10; i++)
		printf("%d  ",v[i]);
	return 0;
}

void fastsort(int v[], int first, int last){
	int i, storeindex;
	void swap(int v[], int i, int j);
	if(first >= last)
		return;  //fewer than two ele
	swap(v, last, (first + last)/2); //move partition elem
	storeindex =  first;
	for(i = first; i <= last-1; i++)
		if(v[i] <= v[last])
			{
				swap(v, storeindex, i);
				storeindex += 1;
			}
	swap(v, last, storeindex);
	fastsort(v, first, storeindex - 1);
	fastsort(v, storeindex + 1, last);
}

/*swap:interchange v[i] and v[j]*/
void swap(int v[], int i, int j){
	int temp;
	temp = v[j];
	v[j] = v[i];
	v[i] = temp;
}

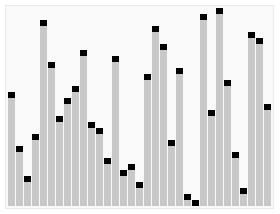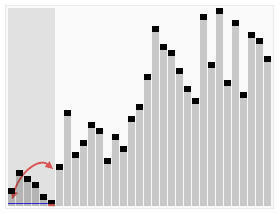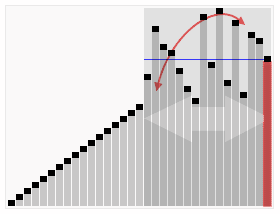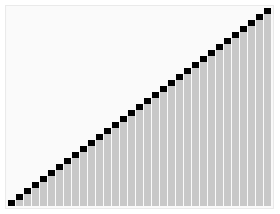
实例分析

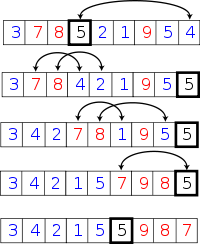
（1）取5作为pivot，然后将其移动到最后一个位置

（2）从第一个数3到倒数第二个数5分别和pivot比较，如果小于等于pivot的数依次从前向后排

（4）将pivot 5移回两个分区中间