【机器学习】反向传播算法 BP

知识回顾

1：首先引入一些便于稍后讨论的新标记方法：

假设神经网络的训练样本有m个，每个包含一组输入x和一组输出信号y，L表示神经网络的层数，S表示每层输入的神经元的个数，SL代表最后一层中处理的单元个数。

之前，我们所讲到的，我们可以把神经网络的定义分为2类：

1）二元分类：SL = 1,其中y = 1 或 0

2）多元分类：当有K中分类时候，SL = K，其中yi = 1表示分到第i类（k>2)

2：再让我们回顾之前所讲到的逻辑回归问题中的代价函数

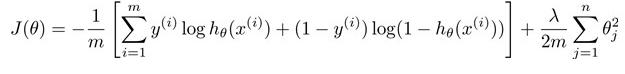
在逻辑回归中，我们只有一个输出变量，但是再神经网络问题中，我们可以有多个输出变量，因此h函数是一个k维的向量（hΘ（x）∈R^k)，并且我们训练集中的因变量是一个同等维度的向量，因此代价函数为

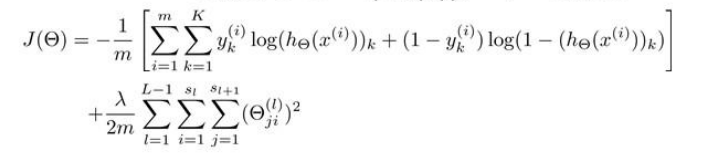
这个函数和之前的逻辑回归基本相同，不同之处是对于每一个特征，我们都会给出一个预测，基本上对每一个特征预测K个不同的结果，然后利用循环在K个预测中我们选择可能性最高的一个，将其与y中的实际数据进行比较。

归一化的那一项只是排除每一层Θ0后，每一层的Θ矩阵和最里层的循环j循环所有的行，循环i则循环所有的列。

即：hΘ(x)与真实值之间的距离为每个样本-每个类输出的加和，对参数进行正则化的偏置项处理所有参数的平方和。

反向传播算法的介绍

反向传播（英语：Backpropagation，缩写为BP）是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。该方法计算对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。反向传播要求有对每个输入值想得到的已知输出，来计算损失函数梯度。因此，它通常被认为是一种监督式学习方法，虽然它也用在一些无监督网络（如自动编码器）中。它是多层前馈网络的Delta规则的推广，可以用链式法则对每层迭代计算梯度。反向传播要求人工神经元（或“节点”）的激励函数可微。

之前，我们在神经网络预测结果的时候，我们采用了一种正向传播的方法，我们从第一层开始，依次计算，直到算出最后一层的hΘ（x）。现在，为了计算出代价函数的偏导数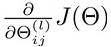，我们需要采用一种反向传播的方法，来计算出网络中所有权重计算损失函数的梯度，也就是，我们首先计算出最后一层的误差，然后再一层层的反向求出上一次层的误差，直到第二层结束。

例如，我们现在有训练集合{x(1),y(1)}，我们的神经网络是一个四层的神经网络，其中K = 4,SL = 4,L =4;

我们首先用向前传播的方法计算出hΘ（x）。

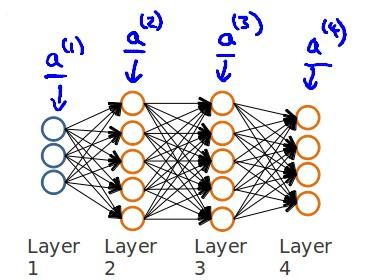
如图所示：

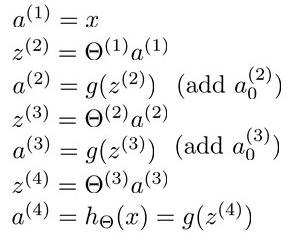
我们在计算的误差时，误差的激活单元的预测a（4）与实际值y（k）之间的误差k = 1：K。

若我们用δ来表示误差，则δ（4） = a（4） - y

向前推：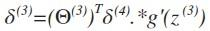

其中g‘（z(3)）是s形函数的导数，即就是g’（z(3))= a（3）.*(1-a(3))。而Θ（3）T δ(4）则是权重导致的误差的和。接下来同理计算第二层的误差。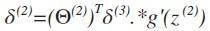

因为第一层是输入变量，所有没有误差。

这时我们有了所有误差的表达式，这时候就可以计算代价函数的偏导数了，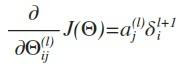

其中l代表目前计算的层数，j代表目前计算的激励单元的下标，即就是下一层的第j个输入变量的下标。i代表下一层中误差单元的下标，即就是收到权重矩阵中第i行影响的下一层中个的误差单元的下标。

如果我们这时候再考虑归一化的处理，就需要计算每一层的误差单元的偏导数，计算每一层的误差单元。但是我们需要为整个训练集计算误差单元，此时的误差单元就是一个矩阵，我用△ (l)ij表示第l层的第i个激励单元受到第j个参数的影响而导致的误差。

算法表示为

即首先用正向传播算法计算出每一层的激励单元，利用训练集的结果与神经网络预测的结果求出最后一层的误差，然后反向的计算出前一层的误差，直到第二层。在求出 △ (l)ij后，我们就可以就按代价函数的偏导数了。

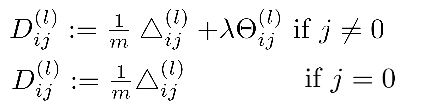
在octave中，我们要用fminuc来求出权重矩阵，我们就需要将矩阵展开为向量，再利用算法求出最优解，然后转换回矩阵，假设我们有三个权重的矩阵，可以用reshape函数实现。

为了更加直观的理解反向传播算法，我们举一个栗子，加入我有如图所示的神经网络结构：

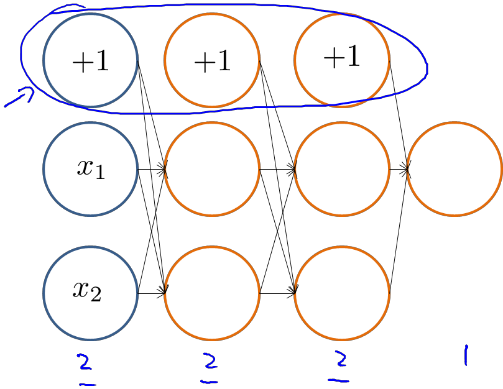
我们可以得出

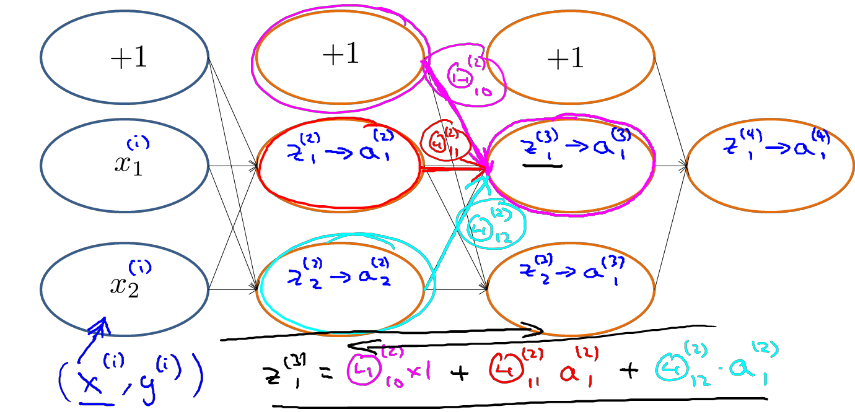
根据正向传播方法，我们可以得出z1(3）的结果。

反向传播算法可以总结为两个步骤

step1：

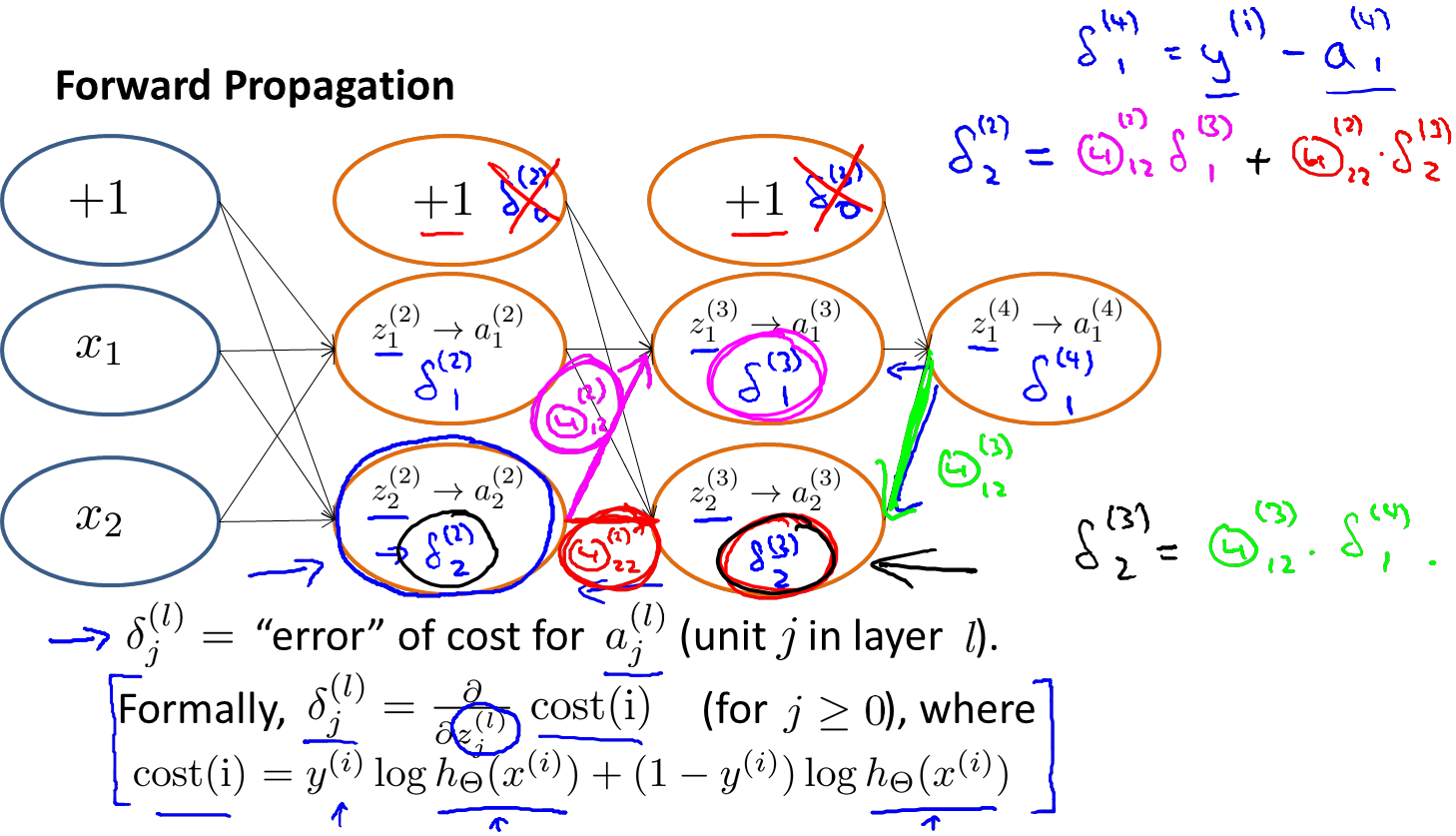
计算这些δ(i)j项，可以看做是激励值的误差，a(l)j（表示第l层中的第j项）

δ(i)j = “error”of cost for a(l)j

step2:

δ(i)j 是关于z(l)j的偏微分

 初始化网络权值（通常是小的随机值）
  do
     forEach 训练样本 ex
        prediction = neural-net-output(network, ex)  // 正向传递
        actual = teacher-output(ex)
        计算输出单元的误差 (prediction - actual)
        计算 

\Delta w_{h}  对于所有隐藏层到输出层的权值                           // 反向传递
        计算 

\Delta w_{i}  对于所有输入层到隐藏层的权值                           // 继续反向传递
        更新网络权值 // 输入层不会被误差估计改变
  until 所有样本正确分类或满足其他停止标准
  return 该网络

　　对这该算法的数学理解是 代价函数关于中间项的偏微分，他们度量着对神经网络中的权值做多少的改变，对中间计算量的影响。

δ（4)1 = y（i）-a（4)1

例如，现在需要计算δ（2)2

根据上图，我们可以得出和δ（2)2有关系的参数是Θ（2)1 2->z(3)1 ->a(3)1-Θ（3)1 1->z(4)1->a(4)1 以及参数Θ（2)2 2 ->z(3)2->a(3)2-Θ(3)1 2->z(4)1->a(4)1  则 δ（2)2 = Θ（2)1 2 δ（3)1 + Θ（2） 2  2δ（3)2

δ（3)2 = Θ（3)1 2 δ（4)1

δ（3)1 = Θ（3）1 1δ（4)1

以上内容是我们怎样用反向传播算法计算代价函数的导数。现在我们需要解决如何吧参数矩阵展开成向量，以便在高级优化步骤中使用。

参数展开

function[jVal,gradient] = cost Function(theta)
...

optTheta = fminunc(@costFunction,initialTheta,options)

　　当我们假设L = 4时，Θ(1)，Θ（2），Θ（3） = matrices(Theta1,Theta2,Theta3)

D(1),D(2),D(3) = matrices(Theta1,Theta2,Theta3)

eg1:

eg2:假设有初始参数值Θ（1），Θ（2），Θ（3），我们选取这些参数展开成一个长向量，称作"initialtheta",作为参数传入fminunc，步骤如下：

step1：用thetaVec重组Θ（1）Θ（2）Θ（3） 此处调用reshape函数

step2：正向传播/反向传播，得到D（1），D（2），D（3）和J（Θ）

step3：取出导数值D(1),D(2),D(3),展开与0相同的顺序，得到gradientVec