[PKUWC2018]猎人杀

---

题解

感觉是一道神题,想不出来

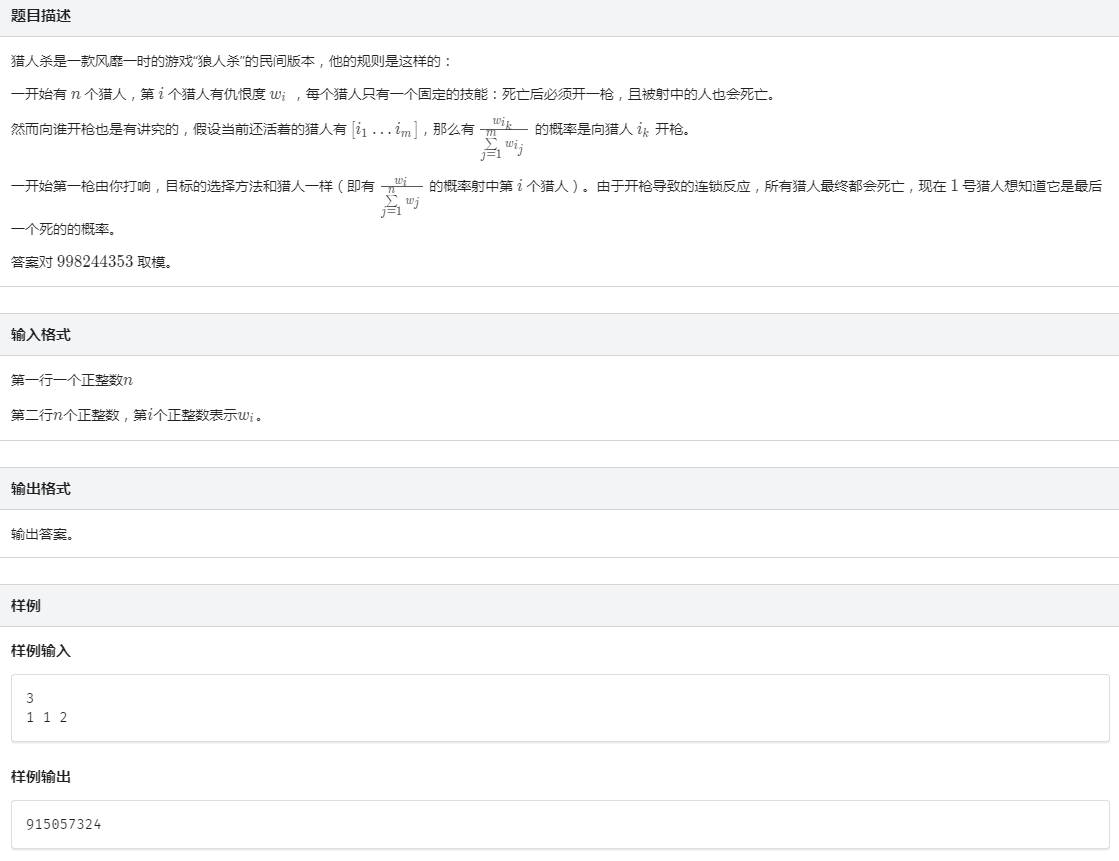
问最后\(1\)号猎人存活的概率

发现根本没法记录状态

每次转移的分母也都不一样

可以考虑这样一件事情:

如果一个人被打中了

那么不急于从所有人中将ta删除,而是给ta打上一个标记,然后继续保留

下一回合如果打中的是一个已经死掉的就继续打

直到打到一个活的为止

可以发现这玩意儿可以是一个无限的东西

那么什么东西是收敛的可以求无线项的值?

等比数列!

那么我们就可以将分母确定下来了

考虑一个容斥:

枚举一个集合\(S\)表示的是至少有这\(i\)个人在1号猎人被打死之后才被打死

用\(W\)表示选定的这个集合的权值和,\(w_1\)表示1号猎人的权值,\(Sum\)表示总权值和

那么这个东西对答案的贡献就是

\((-1)^{|S|}\sum_{i=0}^{inf}{(1-\frac{W+w_1}{Sum})^i\frac{w_1}{W+w_1}}\)

也就是前i枪去打那些没有被钦定的猎人,打完\(i\)枪之后一枪打死\(1\)号猎人的概率

这玩意儿化简一下，等比数列的和\(=\frac{首项}{1-公比}\)

化出来的就是这个东西\((-1)^{|S|}\sum_{i=0}^{inf}{\frac{w_1}{W+w_1}}\)

那么问题就是怎么计算这个集合的大小以及权值和

我们可以考虑背包

直接求出这种权值和的方案的系数

\(f[i][j]\)表示从前\(i\)个猎人中选择了权值和为\(j\)的系数

因为每次选择一个猎人都会使得符号发生改变

所以\(dp\)式子也就是\(f[i][j]=f[i-1][j]-f[i-1][j-w_i]\)

那么这样就可以得到一个\(O(n^2)\)的dp

考虑生成函数

通过上面的dp可以发现对于每一个点权\(w_i\)

,ta的生成函数就是\(1-x^{w_i}\)

那么答案就是\(\prod(1-x^{w_i})\)

分治一下写个\(NTT\)就过了

代码

#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
# define LL long long
# define ls (now << 1)
# define rs (now << 1 | 1)
const int M = 400005 ;
const int mod = 998244353 ;
const int G = 3 ;
const int Gi = mod / G + 1 ;
using namespace std ;

inline int read() {
	char c = getchar() ; int x = 0 , w = 1 ;
	while(c>'9'||c<'0') { if(c=='-') w = -1 ; c = getchar() ; }
	while(c>='0'&&c<='9') { x=x*10+c-'0' ; c = getchar() ; }
	return x*w ;
}

int n , m , ans ;
int len , lim = 1 , rev[M] , val[M] ;
LL inv[M][2] ;
vector < LL > vec[M] ;
inline LL Fpw(LL Base , LL k) {
	int temp = 1 ;
	while(k) {
		if(k & 1) temp = temp * Base % mod ;
		Base = Base * Base % mod ; k >>= 1 ;
	}
	return temp ;
}

inline void NTT(vector < LL > &A , int unit) {
	for(int i = 0 ; i < lim ; i ++) if(rev[i] > i) swap(A[i] , A[rev[i]]) ;
	for(int mid = 1 ; mid < lim ; (mid <<= 1)) {
		int R = (mid << 1) ; LL W = inv[R][unit] ;
		for(int j = 0 ; j < lim ; j += R) {
			LL w = 1 ;
			for(int k = 0 ; k < mid ; k ++ , w = (w * W) % mod) {
				LL x = A[j + k] , y = w * A[j + k + mid] % mod ;
				A[j + k] = (x + y) % mod ; A[j + k + mid] = (x - y) % mod ;
			}
		}
	}
}
inline void pushup(int now) {
	if(vec[ls].empty()) vec[now] = vec[rs] ;
	else if(vec[rs].empty()) vec[now] = vec[ls] ;
	else {
		int sz = vec[ls].size() + vec[rs].size() ;
		lim = 1 ; len = 0 ;
		while(lim <= sz) lim <<= 1 , ++ len ;
		for(int i = 0 ; i <= lim ; i ++) rev[i] = ((rev[i >> 1] >> 1) | ((i & 1) << (len - 1))) ;
		vec[ls].resize(lim + 1) ; vec[rs].resize(lim + 1) ; vec[now].resize(lim + 1) ;
		NTT(vec[ls] , 1) ; NTT(vec[rs] , 1) ;
		for(int i = 0 ; i <= lim ; i ++)
			vec[now][i] = (vec[ls][i] * vec[rs][i]) % mod ;
		NTT(vec[now] , 0) ; LL tinv = Fpw(lim , mod - 2) ;
		for(int i = 0 ; i <= sz ; i ++)
			vec[now][i] = (vec[now][i] * tinv % mod + mod) % mod ;
		vec[now].resize(sz) ;
	}
	vec[ls].clear() ; vec[rs].clear() ;
}
void Solve(int l , int r , int now) {
	if(l == r) {
		vec[now].resize(val[l] + 1) ;
		vec[now][0] = 1 ; vec[now][val[l]] = -1 ;
		return ;
	}
	int mid = (l + r) >> 1 ;
	Solve(l , mid , ls) ;
	Solve(mid + 1 , r , rs) ;
	pushup(now) ;
}

int main() {
	n = read() ;
	for(int i = 1 ; i <= n ; i ++) {
		val[i] = read() ;
		if(i > 1) m += val[i] ;
	}
	for(int i = 1 ; i <= 400000 ; (i <<= 1)) {
		inv[i][1] = Fpw(G , (mod - 1) / i) ;
		inv[i][0] = Fpw(Gi , (mod - 1) / i) ;
	}
	Solve(2 , n , 1) ;
	for(int i = 0 ; i <= m ; i ++) {
		if(!vec[1][i]) continue ;
		ans = ((ans + vec[1][i] * val[1] % mod * Fpw(i + val[1] , mod - 2) % mod) % mod + mod) % mod ;
	}
	printf("%d\n",ans) ;
	return 0 ;
}