cdq分治入门--BZOJ1492: [NOI2007]货币兑换Cash

n<=100000天，一开始有s块钱，每天股票A价格ai，B价格bi，每天可以做的事情：卖出股票；按A:B=RTi的比例买入股票。问最后的最大收益。股票可以为浮点数，答案保留三位。

用脚指头想想就知道是：某一天全部买进来，某一天全部卖出去，没有说买一半卖一半的。

那就可以dp了，f(i)表示前i天最大收益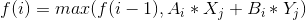，，其中Xi表示用f(i)块钱在第i天能买多少A券，Yi表示f(i)块前第i天买多少B券，可以自己算，n方过不了。

现要找max(Ai*Xj+Bi*Yj)，考虑两个状态j,k,j比k优时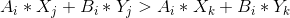

整理得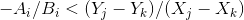，前提是Xj>Xk

那就平衡树维护一下一个递增的(Yj-Yk)/(Xj-Xk)，即维护一个凸包即可，难写，略。

cdq就是这样把一个在线的东西强行转化成离线。

solve(l,r)表示把这个区间里的f算完，solve(l,mid)之后，用(l,mid)的状态更新(mid+1,r)的状态，然后solve(mid+1,r)，这就是一个分治。

为了使这个更新过程顺利完成，在solve(l,mid)时需要找到这个凸包，可以通过维护Xi的单调，然后直接一个栈保存单调的斜率即可；mid+1到r这一段，也需要保证-Ai/Bi的单调，这个可以预处理出来。现在就是一个离线问题，一边凸包单增被离线实现了，一边-Ai/Bi预处理排序好了，那就可以两个指针直接扫一遍更新了。

trick！！(Xj-Xk)可能等于0。。。。。。

 #include<stdio.h>
 #include<string.h>
 #include<stdlib.h>
 #include<algorithm>
 #include<math.h>
 //#include<iostream>
 using namespace std;

 int n,s;
 #define maxn 200011
 double a[maxn],b[maxn],rt[maxn];

 int num[][maxn];
 void mergesort(int L,int R,int cur)
 {
     if (L==R)
     {
         num[cur][L]=L;
         return;
     }
     const int mid=(L+R)>>;
     mergesort(L,mid,cur+),mergesort(mid+,R,cur+);
     int i=L,j=mid+,k=i;
     while (i<=mid && j<=R)
     {
         if (-a[num[cur+][i]]/b[num[cur+][i]]>-a[num[cur+][j]]/b[num[cur+][j]])
             num[cur][k++]=num[cur+][i++];
         else num[cur][k++]=num[cur+][j++];
     }
     while (i<=mid) num[cur][k++]=num[cur+][i++];
     while (j<=R) num[cur][k++]=num[cur+][j++];
 }

 double f[maxn],xx[maxn],yy[maxn];int sta[maxn],top,numf[][maxn];
 double calc(int i,int j) {return fabs(xx[i]-xx[j])>1e-?(yy[i]-yy[j])/(xx[i]-xx[j]):1e300;}
 //i>j
 void solve(int L,int R,int cur)
 {
     if (L==R)
     {
         numf[cur][L]=L;
         f[L]=max(f[L],f[L-]);
         yy[L]=f[L]/(rt[L]*a[L]+b[L]);
         xx[L]=f[L]*rt[L]/(rt[L]*a[L]+b[L]);
         return;
     }
     const int mid=(L+R)>>;
     solve(L,mid,cur+);
     top=;
     for (int i=L;i<=mid;i++)
     {
         const int id=numf[cur+][i];
         while (top> && calc(id,sta[top])-calc(sta[top],sta[top-])>-1e-) top--;
         sta[++top]=id;
     }
     for (int i=mid+,j=;i<=R;i++)
     {
         const int &id=num[cur+][i];
         while (j<top && -a[id]/b[id]-calc(sta[j+],sta[j])<1e-) j++;
         f[id]=max(f[id],a[id]*xx[sta[j]]+b[id]*yy[sta[j]]);
     }
     solve(mid+,R,cur+);
     int i=L,j=mid+,k=i;
     while (i<=mid && j<=R)
     {
         if (xx[numf[cur+][i]]<xx[numf[cur+][j]]) numf[cur][k++]=numf[cur+][i++];
         else numf[cur][k++]=numf[cur+][j++];
     }
     while (i<=mid) numf[cur][k++]=numf[cur+][i++];
     while (j<=R) numf[cur][k++]=numf[cur+][j++];
 }

 int main()
 {
     scanf("%d%d",&n,&s);
     for (int i=;i<=n;i++) scanf("%lf%lf%lf",&a[i],&b[i],&rt[i]);
     mergesort(,n,);
 //    for (int i=0;i<=2;i++){
 //        for (int j=1;j<=n;j++)
 //            cout<<(-a[num[i][j]]/b[num[i][j]])<<' ';cout<<endl;}
     f[]=s;for (int i=;i<=n;i++) f[i]=;
     solve(,n,);
 //    for (int i=1;i<=n;i++) cout<<f[i]<<' ';cout<<endl;
     printf("%.3f\n",f[n]);
     return ;
 }