LSA、LDA

 Latent semantic analysis (LSA) is a technique in natural language processing, in particular distributional semantics, of analyzing relationships between a set of documents and the terms they contain by producing a set of concepts related to the documents and terms. LSA assumes that words that are close in meaning will occur in similar pieces of text (the distributional hypothesis). A matrix containing word counts per paragraph (rows represent unique words and columns represent each paragraph) is constructed from a large piece of text and a mathematical technique called singular value decomposition (SVD) is used to reduce the number of rows while preserving the similarity structure among columns. Words are then compared by taking the cosine of the angle between the two vectors (or the dot product between the normalizations of the two vectors) formed by any two rows. Values close to 1 represent very similar words while values close to 0 represent very dissimilar words.

Occurrence matrix：

LSA can use a term-document matrix which describes the occurrences of terms in documents; it is a sparse matrix whose rows correspond to terms and whose columns correspond to documents. A typical example of the weighting of the elements of the matrix is tf-idf (term frequency–inverse document frequency): the weight of an element of the matrix is proportional to the number of times the terms appear in each document, where rare terms are upweighted to reflect their relative importance.

Rank lowering（矩阵降维）：

After the construction of the occurrence matrix, LSA finds a low-rank approximation to the term-document matrix. There could be various reasons for these approximations:

• The original term-document matrix is presumed too large for the computing resources; in this case, the approximated low rank matrix is interpreted as an approximation (a "least and necessary evil").
• The original term-document matrix is presumed noisy: for example, anecdotal instances of terms are to be eliminated. From this point of view, the approximated matrix is interpreted as a de-noisified matrix(a better matrix than the original).
• The original term-document matrix is presumed overly sparse relative to the "true" term-document matrix. That is, the original matrix lists only the words actually in each document, whereas we might be interested in all words related to each document—generally a much larger set due to synonymy.

Derivation

Let  $X$ be a matrix where element $ (i,j)$ describes the occurrence of term $ i $ in document $j$ (this can be, for example, the frequency). $X$ will look like this:

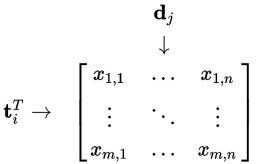
Now a row in this matrix will be a vector corresponding to a term, giving its relation to each document:

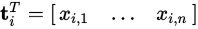
Likewise, a column in this matrix will be a vector corresponding to a document, giving its relation to each term:

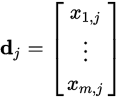
Now, from the theory of linear algebra, there exists a decomposition of $X$ such that $U$ and $ V $ are orthogonal matrices（正交矩阵） and  $\Sigma$  is a diagonal matrix（对角矩阵）. This is called a singular value decomposition (SVD):

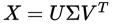
The values  are called the singular values, and  and  the left and right singular vectors. Notice the only part of 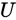 that contributes to 

is the 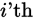  row. Let this row vector be called 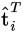. Likewise, the only part of  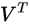that contributes to   is the 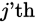 column,.   These are not theeigenvectors,but depend on all the eigenvectors.

https://en.wikipedia.org/wiki/Latent_semantic_analysis