Maximal Discount

Description:

Linda is a shopaholic. Whenever there is a discount of the kind where you can buy three items and only pay for two, she goes completely mad and feels a need to buy all items in the store. You have given up on curing her for this disease, but try to limit its effect on her wallet. You have realized that the stores coming with these offers are quite selective when it comes to which items you get for free; it is always the cheapest ones. As an example, when your friend comes to the counter with seven items, costing 400, 350, 300, 250, 200, 150, and 100 dollars, she will have to pay 1500 dollars. In this case she got a discount of 250 dollars. You realize that if she goes to the counter three times, she might get a bigger discount. E.g. if she goes with the items that costs 400, 300 and 250, she will get a discount of 250 the first round. The next round she brings the item that costs 150 giving no extra discount, but the third round she takes the last items that costs 350, 200 and 100 giving a discount of an additional 100 dollars, adding up to a total discount of 350. Your job is to find the maximum discount Linda can get.

Input:

The input consists of two lines. The first gives the number of items Linda is buying, 1 ≤ n ≤ 100. The next line gives the prices of these items, 1 ≤ pi ≤ 1000.

Output:

Output one line giving the maximum discount Linda can get by selectively choosing which items she brings to the counter at the same time.

Sample Input:

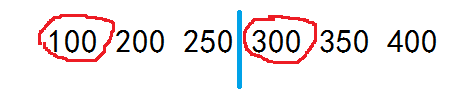
6

400 100 200 350 300 250

Sample Output:

400

---

Hint:

No Hint

---

全英的题目而且挺长的，是不是有点害怕呢？其实只是背景资料有点多~~

将数字排好序后，问题就变得很简单了呢~分析示例：红色圈起来的是可以作为折扣的价钱

原例：

排好序后：

发现，题目中给出的示例刚好是三的倍数，考虑，要不是三的倍数呢？

假如为3k+1，一个示例如下图：

3k+2类似

---

考虑先用数组存储，再排序。

通过上述分析，我们会发现，只要排好序，折扣的价钱分三种情况讨论即可。

但我们会发现，无论n = 3k或者n = 3k + 1或者n = 3k + 2,都只需要输出a[0]+a[3]+...+a[3k]即可。

---

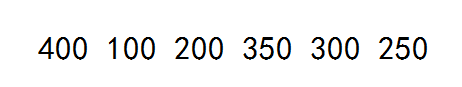
我的代码：

#include<stdio.h>
int main() {
    int n, a[], i, t, min, pi = , j;
    scanf("%d", &n);
    for (i = ; i < n; i++) {
        scanf("%d", &a[i]);
    }
    for (i = ; i < n-; i++) {            // 对数组内的数进行排序~
        min = i;
        for (j = i + ; j < n; j++)
        if (a[min] > a[j])
        min = j;
        if (min != i) {
            t = a[min];
            a[min] = a[i];
            a[i] = t;
        }
    }
    if (n %  == ) {               // 分三类情况讨论（其实你们肯定发现了这没有必要。。。）
        for (i = ; i < n; i += ) {
            pi += a[i];
        }
    }
    else if (n %  == ) {
        for (i = ; i < n; i += ) {
            pi += a[i];
        }
    }
    else if (n %  == ) {
        for (i = ; i < n; i += ) {
            pi += a[i];
        }
    }
    printf("%d\n", pi);
    return ;
}

---

标答：

#include<stdio.h>
#include<stdlib.h>

void Merge(int *R, int low, int m, int high);
void MergeSort(int R[], int low, int high);

int main(void) {
    int arr[], num, i, j, res = ;

    scanf("%d", &num);
    for (i = ; i < num; i++) {
        scanf("%d", &arr[i]);
    }

    // sort the array with Merge Sort.
    MergeSort(arr, , num - );

    for (i = num - , j = ; i >= ; i--, j++) {
        if ((j + )% == ) {
            res += arr[i];
        }
    }

    printf("%d\n", res);
    return ;
}

void Merge(int *R, int low, int m, int high) {
    int i = low, j = m + , p = ;
    int *R1;
    R1 = (int *)malloc((high - low + )*sizeof(i));   // 动态内存分配
    if (!R1) return;

    while (i <= m && j <= high) {
        R1[p++] = (R[i] <= R[j])?R[i++]:R[j++];    // a?b:c的含义是：当a为真时值为b，否则为c
    }

    while (i <= m) {
        R1[p++] = R[i++];
    }

    while (j <= high) {
        R1[p++] = R[j++];
    }

    for (p = , i = low; i <= high; p++, i++) {
        R[i] = R1[p];
    }

    free(R1);      // 用了malloc进行动态内存分配，当内存用完不再需要时需要将其释放
}

void MergeSort(int R[], int low, int high) {
    int mid;
    if (low < high) {
        mid = (low + high)/;
        MergeSort(R, low, mid);
        MergeSort(R, mid + , high);
        Merge(R, low, mid, high);
    }
}

---

给标答加了一些注释，标答效率较高，用了归并排序（有兴趣可以百度~）

看了标答发现分三种情况输出是完全没有必要的，思维不够灵活。。。