1 TypeScript 简介与安装

　　简介：

　　TypeScript 是一种由微软开发维护的自由和开源的编程语言，它是JavaScript的一个超集，支持可选的类型检查，扩展了JavaScript的语法，支持JavaScript的所有语法和语义。

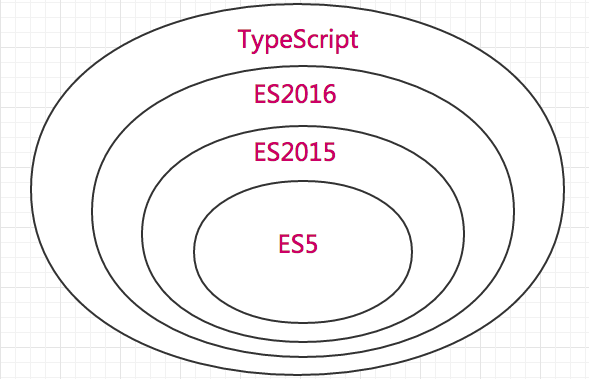
　　ES5、ES2015、ES2016与TypeScript的关系图：

　　安装：

　　我们使用npm来安装TypeScript，首先先确认一下npm的版本，打开终端，输入命令 $ npm - v，检查npm版本，最好是3.0.0以上。(我的是3.10.3，没有安装npm的，自行百度安装)

　　然后执行安装TypeScript命令： $ sudo npm install -g typescript

　　以上命令将会安装TypeScript编译器和可执行程序（tsc），并且添加到环境变量的全局路径中。

　　安装成功截图：

　　

　　（可以运行 $ tsc -v 查看TypeScript版本）

　　TIPS：如果想要指定版本安装，可以执行命令 $ npm install -g typescript@1.8 ，1.8即为版本号。

　　安装完成后我们就可以使用 TypeScript 编译器，名称叫 tsc，可将编译结果生成 js 文件。

　　要编译 TypeScript 文件，可使用如下命令：

　　$ tsc filename.ts

　　编译成功后，就会在相同目录下生成一个同名 js 文件，你也可以通过命令参数来修改默认的输出名称。

　　默认情况下编译器以ECMAScript 3（ES3）为目标但ES5也是受支持的一个选项。TypeScript增加了对为即将到来的ECMAScript 6标准所建议的特性的支持。