P1107 [BJWC2008]雷涛的小猫

题目描述

雷涛同学非常的有爱心，在他的宿舍里，养着一只因为受伤被救助的小猫(当然，这样的行为是违反学生宿舍管理条例的)。在他的照顾下，小猫很快恢复了健康，并且愈发的活泼可爱了。

可是有一天，雷涛下课回到寝室，却发现小猫不见了！经过一番寻找，才发现她正趴在阳台上对窗外的柿子树发呆…

在北京大学的校园里，有许多柿子树，在雷涛所在的宿舍楼前，就有N棵。并且这N棵柿子树每棵的高度都是H。冬天的寒冷渐渐笼罩了大地，树上的叶子渐渐掉光了，只剩下一个个黄澄澄的柿子，看着非常喜人。而雷涛的小猫恰好非常的爱吃柿子，看着窗外树上的柿子，她十分眼馋，于是决定利用自己敏捷的跳跃能力跳到树上去吃柿子。

小猫可以从宿舍的阳台上跳到窗外任意一棵柿子树的树顶。之后，她每次都可以在当前位置沿着当前所在的柿子树向下跳1单位距离。当然，小猫的能力远不止如此，她还可以在树之间跳跃。每次她都可以从当前这棵树跳到另外的任意一棵，在这个过程中，她的高度会下降Delta单位距离。每个时刻，只要她所在的位置有柿子，她就可以吃掉。整个“吃柿子行动”一直到小猫落到地面上为止。

雷涛调查了所有柿子树上柿子的生长情况。他很想知道，小猫从阳台出发，最多能吃到多少柿子？他知道写一个程序可以很容易的解决这个问题，但是他现在懒于写任何代码。于是，现在你的任务就是帮助雷涛写一个这样的程序。

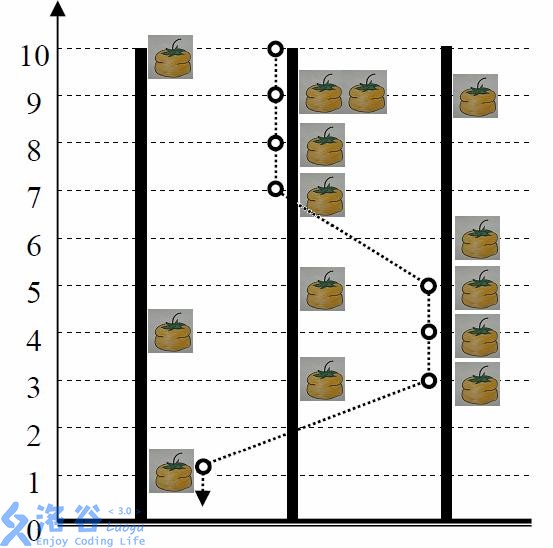
图为N=3,H=10,Delta=2的一个例子。小猫按照图示路线进行跳跃，可以吃到最多的8个柿子

输入输出格式

输入格式：

第一行有三个以空格分隔的整数，分别代表N,H,Delta

接下来的N行，每行第一个整数为Ni，代表第i棵树上的柿子数量。

接下来是Ni个整数，每个整数Tij代表第i棵柿子树的Tij高度上长有一个柿子。

输出格式：

一个整数，即小猫最多吃到的柿子数。

输入输出样例

输入样例#1：

3 10 2

3 1 4 10

6 3 5 9 7 8 9

5 4 5 3 6 9

输出样例#1：

说明

1≤N,H≤2000

0≤Ni≤50000

1≤Delta≤N,1≤Tij≤H

输入文件大小不大于40960KB

来源 Excalibur, 2008

Solution：

　　本题贪心优化dp（话说今天分班考试，炸穿了，作文没写完～物理啥公式都不会～凉凉）。

　　很容易想到本题dp思路，既然和$N,H$有关，那么状态就这俩东西咯，定义$f[i][j]$表示在第$j$棵树的$i$高度能得到的最多果子数，由于每次跳就两种情况，状态转移方程就呼之欲出了：$f[i][j]=max(f[i-1][j],f[i-Delta][k]),k!=j$。

　　但是一个问题是这样的dp是$O(N^2H)$的转移，显然爆掉。

　　发现转移时$f[i-Delta][k]$的最大值是可以确定的，贪心的想到，选的话肯定是从$i-Delta$高度下最多的那棵树转移过来，于是维护$g[i]$表示$i$高度下最多的果子数，每次转移完时维护一下$g$。注意$k!=j$，每次转移先使$f[i][j]=f[i-1][j]$，就不用担心从同一棵树的$i-Delta$转移过来的情况了。

　　目标状态$g[H]$，时间复杂度$O(NH)$，稳妥>._.<。

代码：

/*Code by 520 -- 8.29*/

#include<bits/stdc++.h>

#define il inline

#define ll long long

#define RE register

#define For(i,a,b) for(RE int (i)=(a);(i)<=(b);(i)++)

#define Bor(i,a,b) for(RE int (i)=(b);(i)>=(a);(i)--)

using namespace std;

const int N=;

int n,h,d,a[N][N],f[N][N],g[N],x;

int gi(){

    int a=;char x=getchar();

    while(x<''||x>'')x=getchar();

    while(x>=''&&x<='')a=(a<<)+(a<<)+(x^),x=getchar();

    return a;

}

int main(){

    n=gi(),h=gi(),d=gi();

    For(i,,n) {

        x=gi();

        For(j,,x) a[i][gi()]++;

    }

    For(i,,h){

        For(j,,n) f[i][j]=f[i-][j]+a[j][i];

        if(i>d) For(j,,n) f[i][j]=max(f[i][j],g[i-d]+a[j][i]);

        For(j,,n) g[i]=max(f[i][j],g[i]);

    }

    cout<<g[h];

    return ;

}