机器学习笔记（4）Logistic回归

模型介绍

对于分类问题，其得到的结果值是离散的，所以通常情况下，不适合使用线性回归方法进行模拟。
所以提出Logistic回归模型。
其假设函数如下：
\[
h_θ(x)=g(θ^Tx)
\]
函数g定义如下：
\[
g(z)=\frac{1}{1+e^{-z}}(z∈R)
\]
所以假设函数书写如下：
\[
h_θ(x)=\frac{1}{1+e^{-θ^Tx}}
\]
图像类似如下：

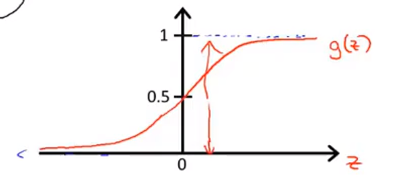
根据图像我们可以看出，当g(z)中的z大于0的时候，其g(z)则大于0.5，则此状态下的可能性则更大。

---

决策边界

对于假设函数h_θ，当确定了其中所有的系数θ，则可以将\(θ^Tx\)绘制出一个用于区分结果值0与1之间的边界。

---

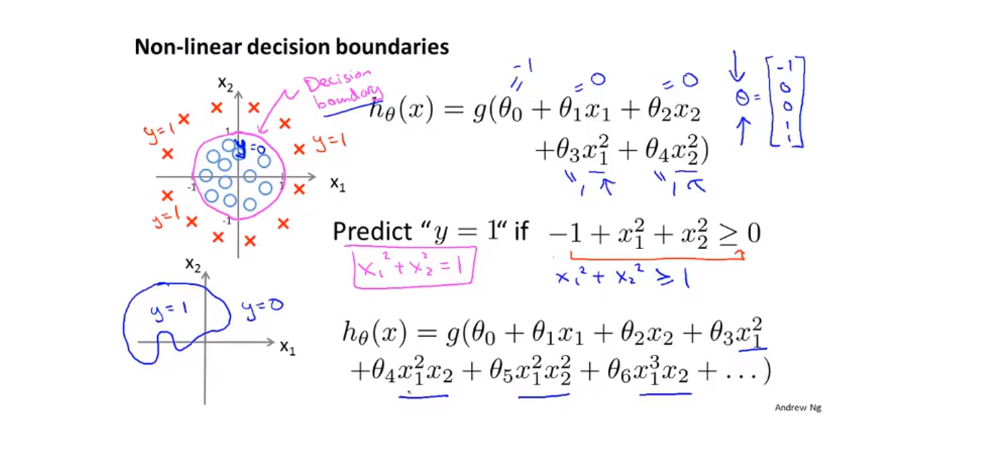
代价函数

和线性回归相同，代价函数可以用于构造最合适的系数θ。
\[
J(θ)=\frac{1}{m}\sum_{i=1}^{m}{cost(h_θ(x)-y)}
\]
\[
cost(h_θ(x)-y)=\begin{cases}
-log(h_θ(x)) & if & y=1 \\
-log(1-h_θ(x)) & if & y=0
\end{cases}
\]

\[
J(θ)=\frac{1}{m}[\sum_{i=1}^{m}{y^{(i)}logh_θ(x^{(i)})+(1-y^{(i)})log(1-h_θ(x^{(i)}))}]
\]

分析

对于cost函数，在y=1的时候，很明显当\(h_θ(x)\)趋近于1的时候，cost函数接近于0，则代价函数\(J(θ)\)也接近于0，合理；\(h_θ(x)\)趋近于0的时候，cost函数趋近于无穷大，而代价函数\(J(θ)\)也趋于无穷大，这是不合理的。从代价函数本身的意义出发，就是寻找当代价函数\(J(θ)\)最小的时候，就得到最合理的系数θ。

---

梯度下降

为了获得最小的\(J(θ)\)
给出：
\[
θ_j:=θ_j-α\frac{∂}{∂θ_j}J(θ)
\]
\[
θ_j:=θ_j-α\frac{1}{m}\sum_{i=1}^{m} {(h_θ(x^{(i)})-y^{(i)})x_j^{(i)}}
\]

通过不断迭代得到最终合适的θ。

---

一对多问题

对于很多分类问题，不只是需要分类为两类0，1，可能需要做更多的分类。

对于解决这类问题可以采用回归分类器，见下图：

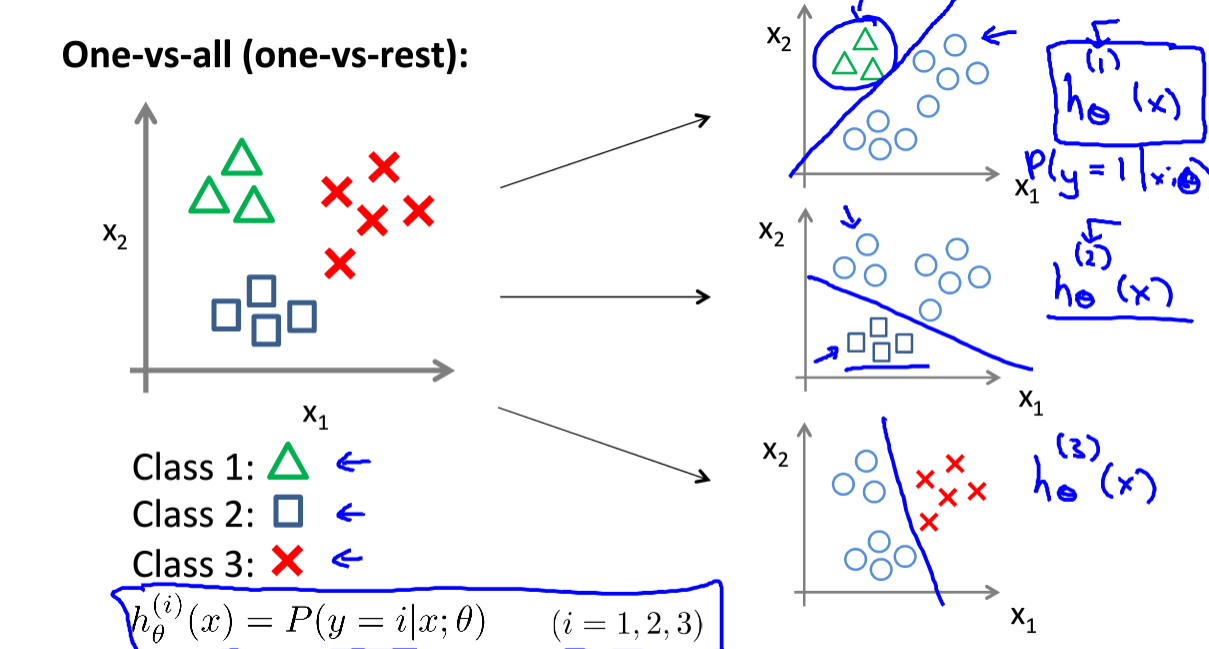
对于多个分类，可以选择将需要判断的那个分类定义为正类，其余都定义为负类，执行logistic回归得到一个假设函数\(h_θ^{(i)}\)，使用时，选择最为合适的假设函数进行模拟即可。

---