HDU 6053 TrickGCD（莫比乌斯反演）

http://acm.hdu.edu.cn/showproblem.php?pid=6053

题意：
给出一个A数组，B数组满足Bi<=Ai。

现在要使得这个B数组的GCD值>=2，求共有多少种情况。

思路：
在比赛的时候筛了素数表，然后枚举GCD来做，但是还是有些重复情况无办法剔除，赛后才知道是要用莫比乌斯来处理的，然后就趁机学习了一下莫比乌斯。

先是枚举GCD，每个数的可选情况就是GCD/a【i】，在这里我们可以把GCD/a【i】相同的数一起处理，也就是用快速幂来计算，这样会显得更快。

那么莫比乌斯是用来干嘛的呢？

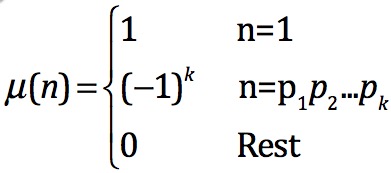
然后就是容斥思想。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn = 1e5 + ;

 const int mod= 1e9+;

 int n;
 int a[maxn];

 ll cnt[maxn];
 ll num[*maxn];

 bool check[maxn+];
 int prime[maxn+];
 int mu[maxn+];

 void Moblus()
 {
     memset(check,false,sizeof(check));
     mu[] = ;
     int tot = ;
     for(int i = ; i <= maxn; i++)
     {
         if( !check[i] ){
             prime[tot++] = i;
             mu[i] = -;
         }
         for(int j = ; j < tot; j++)
         {
             if(i * prime[j] > maxn) break;
             check[i * prime[j]] = true;
             if( i % prime[j] == ){
                 mu[i * prime[j]] = ;
                 break;
             }else{
                 mu[i * prime[j]] = -mu[i];
             }
         }
     }
 }

 ll qpow(ll a, ll b)
 {
     ll ans=;
     while(b)
     {
         if(b&)  ans=(ans*a)%mod;
         a=(a*a)%mod;
         b>>=;
     }
     return ans;
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     Moblus();
     int kase=;
     int T;
     scanf("%d",&T);
     while(T--)
     {
         memset(cnt,,sizeof(cnt));
         scanf("%d",&n);
         int MIN=INF;
         int MAX=;
         for(int i=;i<=n;i++)
         {
             scanf("%d",&a[i]);
             MIN=min(MIN,a[i]);
             MAX=max(MAX,a[i]);
             cnt[a[i]]++;
         }

         num[]=;
         for(int i=;i<=;i++)   num[i]=num[i-]+cnt[i];

         ll ans=;

         for(int i=;i<=MIN;i++)
         {
             ll tmp=;
             for(int j=;j*i<=MAX;j++)
             {
                 tmp=(tmp*qpow((ll)j,num[i*j+i-]-num[i*j-]))%mod;  //快速幂计算，j是GCD的倍数，也就是a【i】/GCD
             }
             ans=(ans-tmp*mu[i]+mod)%mod;
         }

         printf("Case #%d: %I64d\n",++kase,ans);
     }
     return ;
 }