51nod 1098 最小方差 排序+前缀和+期望方差公式

题目：

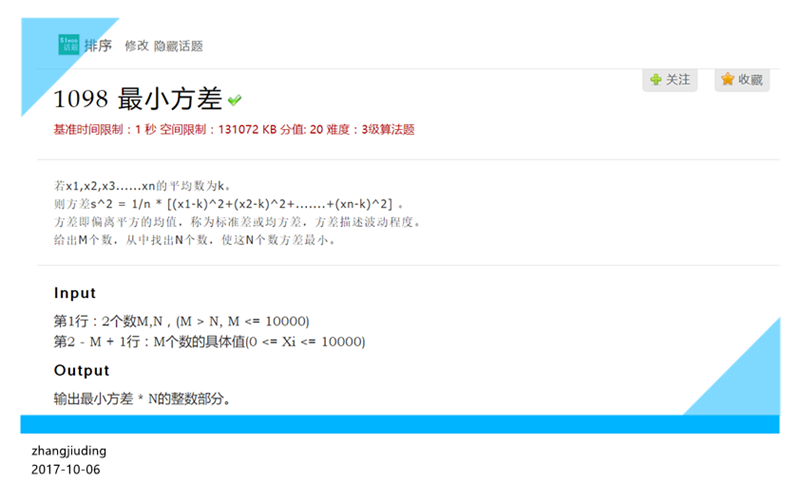
题目要我们，在m个数中，选取n个数，求出这n个数的方差，求方差的最小值。

1.我们知道，方差是描述稳定程度的，所以肯定是着n个数越密集，方差越小。

　　所以我们给这m个数排个序，从连续的n个数中找。

2.方差公式D（x^2） = E（x^2）- E（x）^2;

　　E（x） = x*f(x) dx (从负无穷到正无穷积分)

　　E （x^2） = x^2*f(x) dx (从负无穷到正无穷积分)

3.对于这道题，相当于每个数的权值相同，也就是f(x)相同，都等于1/n。（可以理解f(x)表示概率）

4.我们可以用前缀和来减少时间复杂度。

　　sum1[i]表示前 i 项的和，方便算出E（x）^2

　　sum2[i]表示前 i 项平方和 ，方便算出E（x^2）

　当我们要算第 i 项到第 j 项共 j-i+1 项的方差的时候我们只用这样写：

ll k1 = sum1[j]-sum1[i-];   // 第i项到第j项的和
double s1 = 1.0*k1/n*k1/n;  // k1/n表示平均数E(x), s1表示E(x)^2
ll k2 = sum2[j]-sum2[i-];   // 第i项到第j项的平方和
double s2 = 1.0*k2/n;         // s2 和 k2/n 表示E(x^2)

　　第 i 项到第 j 项的方差就等于 s2-s1 了。

5.我们可以得到大致代码，当然现在就可以直接开始敲了，如果看懂了的话。

    double mn = 2e18;
    for(int i = n;i <= m; i++){
        ll k1 = sum1[i]-sum1[i-n];
        double s1 = 1.0*k1/n*k1/n;
        ll k2 = sum2[i]-sum2[i-n];
        double s2 = 1.0*k2/n;

        mn = min(s2-s1,mn);
    }

6.我们要注意一下精度问题，我的做法是给mn += 1e-8。

代码：

#include <bits\stdc++.h>
using namespace std;
typedef long long ll;

int a[];
ll sum1[];  //sum1[i]表示前i项和
ll sum2[];  //sum2[i]表示前i项平方和
int main() {
  ll m,n;
  cin >> m >> n;
    for(int i = ;i <= m; i++){
        cin >> a[i];
    }

    sort(a+,a++m);  // 排个序，让数字变得紧凑
    for(int i = ;i <= m; i++){
        sum1[i] = sum1[i-] + a[i];
        sum2[i] = sum2[i-] + a[i]*a[i];
    }

    double mn = 2e18;      //存最小的方差
    for(int i = n;i <= m; i++){
        ll k1 = sum1[i]-sum1[i-n];  // 第 i-n+1 项到第 i项共 n 项的和。
        double s1 = 1.0*k1/n*k1/n;  // k1/n表示平均数E(x),s1表示 E(x)^2
        ll k2 = sum2[i]-sum2[i-n];  // 第 i-n+1 项到第 i项共 n 项的和。
        double s2 = 1.0*k2/n;       // k2/n表示E(x^2) 

        mn = min(s2-s1,mn);
    }

    // 如果不加这个可能会出问题，因为cout  double用的是科学记数法，需要消除误差。
    mn += 1e-;
    cout << (ll)(mn*n) << endl;
  return ;
}
//  writen by zhangjiuding