Copying GC (Part one)

目录

• GC复制算法
  • copy()函数 将传递给自己的参数复制，然后递归复制其孩子
  • new_obj()函数
  • 执行过程
  • 优点
  • 缺点
• Cheney的GC复制算法
  • copy()函数
  • 执行过程
  • 被隐藏的队列
  • 优缺点

GC复制算法

Copying GC,Marvin L.Minsky，1963

该算法吧某个空间里的活动对象复制到其他空间，把原空间里的所有对象进行回收。再此我们把复制活动对象的空间称为From空间，将粘贴活动对象的空间称为To空间。

---

先介绍Robert R.Fenichel与Jerome C.Yochelson 研究出的GC复制算法。

GC复制算法是利用From空间进行分配的。当From空间被完全占满时，GC会将活动对象全部复制到To空间。当复制完成后，该算法会把From空间和To空间互换GC也就结束了。From空间和To空间大小必须一致。这是为了保证能把From空间中的所有活动对象都收纳到To空间里。如下图所示：

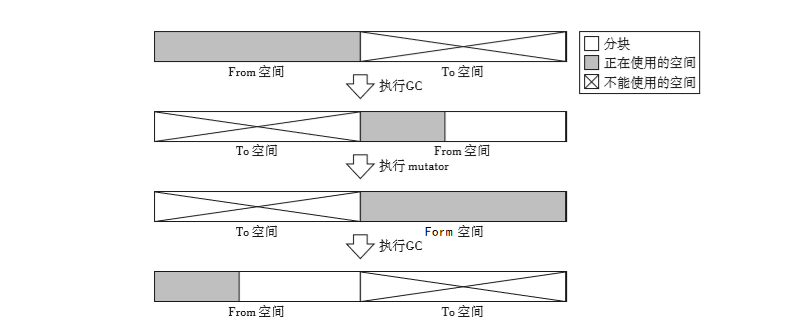
下面是GC复制算法的copying()函数

copying(){
    $free = $to_start
    for(r :$roots)
        *r = copy(*r)
    swap($from_start, $to_start)
}

$free 是指示分块开头的变量。先将$free设置To空间的开头，然后从根开始引用复制对象。copy()函数将作为参数传递的对象*r复制的同时，也将其子对象进行递归复制。复制结束后返回指针，这里返回的指针指向的是*r所在的新空间对象。

在GC结束时,原空间的对象会作为垃圾被回收。因此，由根指向原空间对象的指针也会被重写成指向返回值的新对象的指针。

copy()函数 将传递给自己的参数复制，然后递归复制其孩子

copy(obj){
    if(obj.tag != COPIED)
        copy_data($free, obj, obj.size)
        obj.tag = COPIED
        obj.forwarding = $free
        $free += obj.size
        for(child :children(obj.forwarding))
            *child = copy(*child)
    return obj.forwarding
}

• 首先检测obj是否复制过？这里使用了obj.tag 是obj的一个域。如果是COPIED就是复制过。
• 如果没有被复制，函数会复制obj，返回指向新空间对象的指针。如果已经复制则函数会返回新空间对象的地址。

---

使用copy_data()将函数复制到$free指示的空间

如图示，对象A复制生成了A^'。新空间$free，大小时size，这时候新对象的指针还是指向C,D（from空间）。

之后给该对象的tag改为COPIED，这样即使被多个对象引用也不会复制多次。

把指向新空间对象的指针放在obj.forwarding里。之后当找到指向原空间对象的指针时，需要把找到的指针换到新空间，forwarding 指针正是为此准备的。如图所示

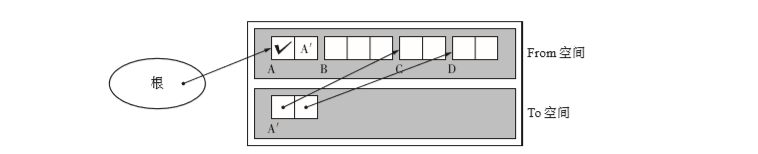
• 可以看到图中From空间A的A^'， 我们需要更换根指针时，只需要让根的指向，变为A^'即可。
• 可以看到A多个一个对号，这个对号就是标记COPIED.
• 按照obj长度向前移动$free，递归调用copy()函数。

这样一来，To空间指向From空间的指针就全部指向To空间了。如下图示。

A、C、D 保持着原有的引用关系被从From空间复制到了To空间。从根指向A的指针也被换成了AꞋ。留在From空间里的A到D都被回收了。

要实现这个方法有两个条件，首先每个对象必须有2个域用作COPIED,forwarding。接下来COPYED标签为了挪动obj中的域，必须选1个mutator绝对不会用到的值。

new_obj()函数

new_obj(size){
    if($free+size > $from_start + HEAP_SIZE/2) //判断是否有空间
        copying() //没有的话进行GC复制压缩
        if($free+size > $from_start + HEAP_SIZE/2) //在此判断空间
            allocation_fail()  //分配失败
    obj = $free  //分配成功
    obj.size = size
    $free += size
    return obj
}

• HEAP_SIZE 表示的是把 From 空间和 To 空 间加起来的大小
• 如果分块足够大，那么程序就会把size大小的空间从这个分块中分割出来交给mutator。别忘了还得把$free移动size个长度。

执行过程

假设堆里对象的配置如下图事先将$free指向To开头。

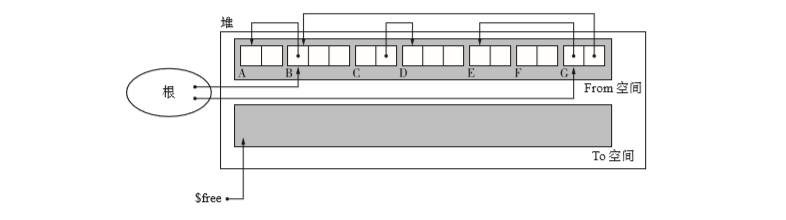
• 首先直接被根引用的对象B和G，B先被复制到了To空间。如下图。
  
  

• 我们将B被复制后的对象称为 BꞋ，对B标记上COPIED和forwarding。

• 下面我们要把还在From空间里的A复制到To。如下图
  
  

• 这才是完成了B的复制，因为A没有子对象所以对A的复制也就完成了。

• 接下来就是要复制同样是被根引用的G了及其孩子对象。

• B，E均是G的孩子，但是B已经被复制过，所以只要把从G指向B的指针换到BꞋ上就行了。

• 最后只要把 From 空间和 To 空间互换，GC 就结束了。
  
  

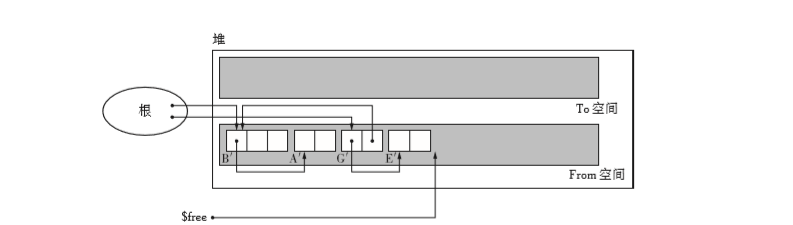
• 其中C,D,F没办法查找，所以会被回收掉。

• 这里的搜索顺序是B,A,G,E。其实也可以分为广度优先和深度优先。

优点

1. 优秀的吞吐量：

标记清除算法消耗吞吐量的是搜索活动对象(标记)和搜索整体堆(清除)。

GC复制算法只搜索并复制活动对象。能在较短时间内完成GC。堆越大相比之下性能约明显。但是还是和对象数量成正相关。

1. 可实现高速分配：

GC复制算法不使用空闲链表，而是使用连续的内存空间。所以相比标记清除算法来说，GC复制算法会很快速的分配。因为标记清除最坏的情况是每次分配都在队尾进行处理。

1. 不会发生碎片化：

活动对象被集中安排在 From 空间的开头对吧。像这样把对象重新集中，放在堆的一端的行为就叫作压缩。在GC复制算法中，每次运行GC时 都会执行压缩。 因为压缩的原因，所以不会产生碎片化。(当然标记清除算法也可以通过压缩来解决碎片化问题。)

1. 与缓存兼容：

GC复制算法中有引用关系的对象离得比较近。这种情况下mutator的速度会非常快，通过压缩来吧有引用关系对象安排在堆中较劲的位置。(其实这些东西在设计项目的时候感觉都用得上。)

缺点

1. 堆使用效率低下

GC复制将内存二等分，利用率最高是50%，最低的话可想而知。我们可以通过GC复制搭配标记清除来改善这一点。后期面会介绍的详细一点。

1. 不兼容保守式GC算法

GC标记清除和保守式GC兼容，因为GC标记清除不能移动对象。而GC复制算法则是全部移动，重写指针。不过GC复制算法和保守式GC算法可以进行组合这一点在后面保守式GC会提到。

1. 递归调用函数

复制某个对象时要递归复制它的子对象。因此在每次进行复制的时候都要调用函数，由此带来的额外负担不容忽视。大家都知道比起这种递归算法，迭代算法更能高速地执行，因为在每次递归调用时都会消耗栈，所以还有栈溢出的可能。将在后面Cheney的GC复制算法中提到，

在循环的次数较大的时候，迭代的效率明显高于递归（比如计算40个斐波那契数会是3-4倍的时间差距。）。迭代就是代码段的循环，例如计算斐波那契通过for循环来进行只不过是吧上次计算的值保存后再次使用。递归是是要去建立新的副本的，会消耗大量的内存和时间，而迭代反复调用同一块函数的内存。

Cheney的GC复制算法

C.J.Cheney, 1970

相比Fenichel和Yochelson的GC复制算法，Cheney使用迭代而不是递归。

copying(){
    scan = $free = $to_start
    for(r :$roots)
        *r = copy(*r)
    while(scan != $free)
        for(child :children(scan))
            *child = copy(*child)
        scan += scan.size
    swap($from_start, $to_start)
}

• 先将scan和$free两个指针初始化。scan是用于搜索复制完成的对象的指针。$free是指向分块开头的指针。
• 首先复制的是直接从根引用的对象。然后搜索复制完成的对象，迭代的去复制其子对象。
• 最后把From和To互换。关键点仍是copy().

copy()函数

copy(obj){
    if(is_pointer_to_heap(obj.forwarding, $to_start) == FALSE)
        copy_data($free, obj, obj.size)
        obj.forwarding = $free
        $free += obj.size
    return obj.forwarding
}

• 先检查是否复制完毕，对于is_pointer_to_heap(obj.forwarding, $to_start)，如果obj.forwarding指向To，则返回True，否则返回FALISE.
• 复制对象，并对forwarding指针进行设定。

Cheney的GC复制算法并没有使用到COPYIED标签而是使用forwarding指针。那么forwarding指针是如何判断是否复制完毕呢？在没有复制之前，指针指的的From区域，在复制完后指针指的的To区域，很明显我们可以通过forwarding指针来区分。

执行过程

引入了scan指针。下面是堆的初始状态。

• 首先福之所有从根直接引用的对象，这里就是BG。

• 这时候scan指着To的开头，$free向右移动B.size+G.size。关键是scan每次对复制完成的对象搜索时，以及$free每次对没复制的对象复制时，向右移动。至scan和$free一直。
• 下面对 BꞋ 进行搜索。

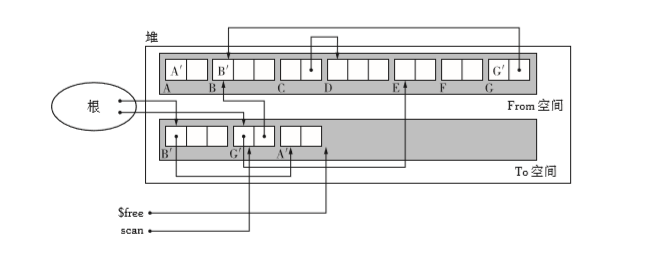
• 搜索 BꞋ ，然后把被 BꞋ引用的A复制到了To。同时把scan和$free右移动。
• 下面是搜索GꞋ,之后E被复制到了To，从GꞋ指向B的指针换到了 BꞋ。
• 之后就改搜索 AꞋ和 EꞋ了，不过他们没有子对象，所以不能进行复制。此时scan和$free一致，所以最后交换空间GC就结束。

我们看到了，scan和$free向右移动不是同步的，我们之前说过，单纯的吧B变为BꞋ是没有复制完成的，但是为了存储$free还要向后移位。此时没有复制完所以scan不搜索对象，所以不移位。

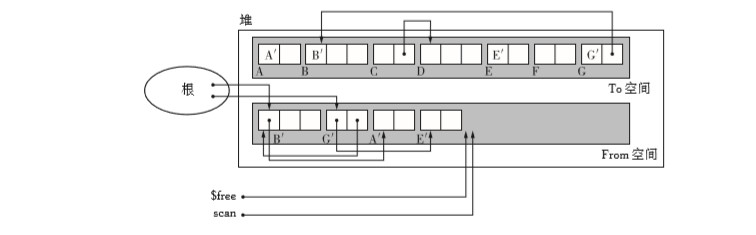
按B.G.A.E的顺序来搜索对象，采用的是广度优先

被隐藏的队列

广度优先需要FIFO结构队列支持，需要把搜索对象保存到队列中一遍搜索一边取出。但是我们要怎么进行呢？

实际上scan和$free之间的堆变成了队列。scan左边是已经搜索完毕的空间，$free每次右移，队列里就会增加对象。scan每次右移队列里就会取出对象。这样就能满足FIFO的条件。这样我们就不用去设置单独的队列实现功能了。

优缺点

优点：使用迭代算法，减少了函数的调用和额外的栈消耗。省去了用于搜索内存空间这一点。

缺点：我们可以从图中看出，复制的对象之间有引用关系，但是他们相邻的程度随着对象的增多而减少。这就不利于缓存的使用了。因此说，它的缓存兼容性没有深度优先的GC复制算法好。只能说比起标记清除和引用计数来说好一些。