（转载） 天梯赛 L2-018. 多项式A除以B

题目链接

题目描述

这仍然是一道关于A/B的题，只不过A和B都换成了多项式。你需要计算两个多项式相除的商Q和余R，其中R的阶数必须小于B的阶数。

输入格式：

输入分两行，每行给出一个非零多项式，先给出A，再给出B。每行的格式如下：

N e[1] c[1] ... e[N] c[N]

其中N是该多项式非零项的个数，e[i]是第i个非零项的指数，c[i] 是第i个非零项的系数。各项按照指数递减的顺序给出，保证所有指数是各不相同的非负整数，所有系数是非零整数，所有整数在整型范围内。

输出格式：

分两行先后输出商和余，输出格式与输入格式相同，输出的系数保留小数点后1位。同行数字间以1个空格分隔，行首尾不得有多余空格。注意：零多项式是一个特殊多项式，对应输出为“0 0 0.0”。但非零多项式不能输出零系数（包括舍入后为0.0）的项。在样例中，余多项式其实有常数项“-1/27”，但因其舍入后为0.0，故不输出。

输入样例：

4 4 1 2 -3 1 -1 0 -1

3 2 3 1 -2 0 1

输出样例：

3 2 0.3 1 0.2 0 -1.0

1 1 -3.1

分析：

首先看一下多项式的除法计算

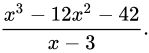
把被除式、除式按某个字母作降幂排列，并把所缺的项用零补齐，写成以下这种形式：

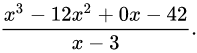
然后商和余数可以这样计算：

1.将分子的第一项除以分母的最高次项（即次数最高的项，此处为x）。结果写在横线之上(x^3 ÷ x = x^2).

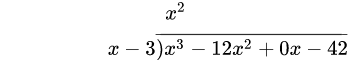
2.将分母乘以刚得到结果（最终商的第一项），乘积写在分子前两项之下（同类项对齐） (x^2 · (x − 3) = x^3 − 3x^2).

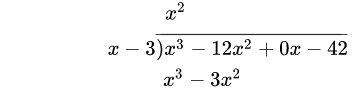
3.从分子的相应项中减去刚得到的乘积（消去相等项，把不相等的项结合起来），结果写在下面。((x^3 − 12x^2) − (x^3 − 3x^2) = −12x^2 + 3x^2 = −9x^2)然后，将分子的下一项“拿下来”。

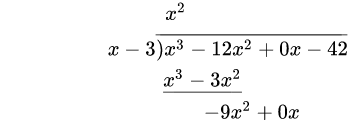
4.把减得的差当作新的被除式，重复前三步（直到余式为零或余式的次数低于除式的次数时为止．被除式=除式×商式+余式 ）

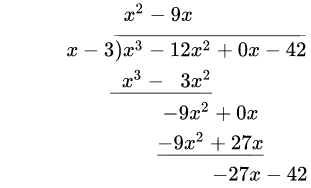
5.重复第四步。这次没什么可以“拿下来”了。

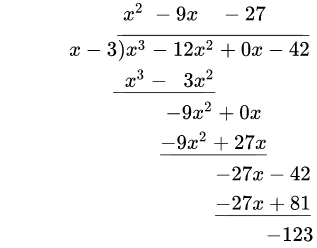
横线之上的多项式即为商，而剩下的 (−123) 就是余数。

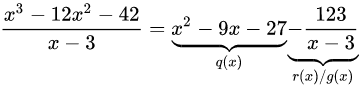
算数的长除法可以看做以上算法的一个特殊情形，即所有 x 被替换为10的情形。

除法变换[编辑]

使用多项式长除法可以将一个多项式写成 除数-商 的形式（经常很有用）。 考虑多项式 P(x), D(x) （(D)的次数 < (P)的次数）。 然后，对某个商多项式 Q(x) 和余数多项式 R(x) （(R)的系数 < (D)的系数），

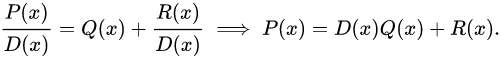
这种变换叫做除法变换，是从算数等式 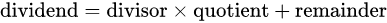得到的。

应用[编辑]

多项式的因式分解[编辑]

有时某个多项式的一或多个根已知，可能是使用有理数根定理得到的。如果一个n次多项式P(x)的一个根r已知，那么P(x) 可以使用多项式长除法因式分解为(x-r)Q(x)}的形式，其中Q(x)是一个n-1次的多项式。简单来说，Q(x)就是长除法的商，而又知r是P(x)的一个根、余式必定为零。

相似地，如果不止一个根是已知的，比如已知r和s这两个，那么可以先从P(x)中除掉线性因子x-r得到Q(x)，再从Q(x)中除掉 x-s，以此类推。或者可以一次性地除掉二次因子x^2-(r+s)x+rs。

使用这种方法，有时超过四次的多项式的所有根都可以求得，虽然这并不总是可能的。例如，如果有理数根定理可以用来求得一个五次方程的一个（比例）根，它就可以被除掉以得到一个四次商式；然后使用四次方程求根的显式公式求得剩余的根。

寻找多项式的切线[编辑]

多项式长除法可以用来在给定点上查找给定多项式的切线方程。[2] 如果 R(x) 是 P(x)/(x-r)2 的余式——也即，除以 x^2-2rx+r2——那么在 x=r 处 P(x) 的切线方程是 y=R(x)，不论 r 是否是 P(x) 的根。

代码：

#include<iostream>
#include<string>
#include<stdio.h>
#include<string.h>
#include<map>
#include<queue>
#include<math.h>
#include<algorithm>
using namespace std;
const int maxn=1e6+100;
int x,lena,lenb,maxa=-1,maxb=-1,cntc,cnta;
double y,a[maxn],b[maxn],c[maxn];
int input(int len,double *arr, int *maxx){
    for(int i=0;i<len;++i){
        scanf("%d%lf",&x,&y);
        arr[x]=y;
        *maxx=max(*maxx,x);
    }  

}
void clearzoro(int &cnt,int be,double *arr){
    cnt=0;
    for(int i=be;i>=0;--i){
        if(!fabs(arr[i])<1e-8)
            fabs(arr[i])<0.05?arr[i]=0.0:cnt++;
    }
}
void output(int cnt,int be,double *arr){
    if(cnt==0) puts("0 0 0.0");
    else {
        printf("%d",cnt);
        for(int i=be;i>=0;--i){
            if(!fabs(arr[i])<1e-8) printf(" %d %.1lf",i,arr[i]);
        }
        puts("");
    }
}  

int main(){  

    scanf("%d",&lena);
    input(lena,a,&maxa);
    scanf("%d",&lenb);
    input(lenb,b,&maxb);
    for(int i=maxa;i>=maxb;--i){
        c[i-maxb]=a[i]/b[maxb];
        for(int j=maxb;j>=0;--j)
            a[j+i-maxb]-=b[j]*c[i-maxb];
    }
    clearzoro(cntc,maxa-maxb,c);
    clearzoro(cnta,maxb,a);
    output(cntc,maxa-maxb,c);
    output(cnta,maxb-1,a);
    return 0;
}