leetCode 41.First Missing Positive (第一个丢失的正数) 解题思路和方法

First Missing Positive 



Given an unsorted integer array, find the first missing positive integer.



For example,

Given [1,2,0] return 3,

and [3,4,-1,1] return 2.

Your algorithm should run in O(n) time and uses constant space.

思路：这个题刚開始是没有思路的，难就难在O(n)时间内常数量空间，所以此题较为考察思维敏捷性。其解题核心思想是将数组的第i位存正数i+1。最后再遍历一次就可以。

其它人的思想，我也是看了这个思想自己写的代码。

尽管不能再另外开辟很数级的额外空间，可是能够在输入数组上就地进行swap操作。

思路：交换数组元素。使得数组中第i位存放数值(i+1)。

最后遍历数组，寻找第一个不符合此要求的元素，返回其下标。整个过程须要遍历两次数组，复杂度为O(n)。

下图以题目中给出的第二个样例为例，解说操作过程。

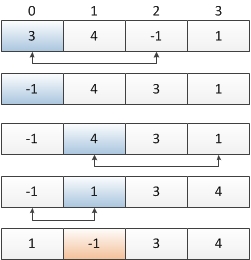
妈蛋。这题挣扎好久。

首先思路上，其次临界条件，这题和以下题异曲同工：

n个元素的数组，里面的数都是0~n-1范围内的，求数组中反复的某一个元素。没有返回-1, 要求时间性能O(n) 空间性能O(1)。

代码还是比較简单。例如以下：

public class Solution {
    public int firstMissingPositive(int[] nums) {
        if(nums.length == 0)
            return 1;
        //第i位存放i+1的数值
        for(int i = 0; i < nums.length;i++){
            if(nums[i] > 0){//nums[i]为正数，放在i+1位置
                //假设交换的数据还是大于0且<i+1，则放在合适的位置,且数据不相等，避免死循环
                //这个while是关键，其它都是没有难度的
                while(nums[i] > 0 && nums[i] < i+1 && nums[i] != nums[nums[i] -1]){
                    int temp = nums[nums[i]-1];//交换数据
                    nums[nums[i]-1] = nums[i];
                    nums[i] = temp;
                }
            }
        }
        //循环寻找不符合要求的数据，返回
        for(int i = 0; i < nums.length;i++){
            if(nums[i] != i+1){
                return i+1;
            }
        }
        //假设都符合要求，则返回长度+1的值
		return nums.length + 1;
    }
}