poj3207 2-SAT入门

一开始题意没读懂 = =

题意：比如说对于表盘上a到b、c到d都要连边，这两个边不能交叉。这两个边要么都在圆内要么都在圆外，而且可以是曲线= =

比如这种情况：（Reference：http://blog.csdn.net/l04205613/article/details/6668318）

（左边情况看似是合法的，但是一个边在圆内一个在圆外，形成矛盾了）

这回只需判断是否可行不用输出方案，这样就简单多了

STEP：构图，矛盾的地方连边->tarjan求scc->判断是否a和not a在同一分量内

 #include "iostream"
 #include "cstring"
 #include "stack"
 using namespace std;
 #define maxn 2010

 int G[maxn][maxn],dx[maxn],dy[maxn];
 int pre[maxn],lowlink[maxn],sccno[maxn];
 int dfs_clock,scc_cnt,N,M;
 stack<int> St;

 void tarjan(int u)
 {
     pre[u]=lowlink[u]=++dfs_clock;
     St.push(u);
     for (int i=;i<=G[u][];i++)
     {
         int v=G[u][i];
         if (!pre[v])
         {
             tarjan(v);
             lowlink[u]=min(lowlink[u],lowlink[v]);
         }
         else if (!sccno[v])
         {
             lowlink[u]=min(lowlink[u],pre[v]);
         }
     }
     if (lowlink[u]==pre[u])
     {
         scc_cnt++;
         for (;;)
         {
             int x=St.top();
             St.pop();
             sccno[x]=scc_cnt;
             if (x==u) break;
         }
     }
 }

 void find_scc(int n)
 {
     dfs_clock=scc_cnt=;
     memset(sccno,,sizeof(sccno));
     memset(pre,,sizeof(pre));
     for (int i=;i<=n;i++)
         if (!pre[i])
             tarjan(i);
 }

 void add_edge(int x,int y)
 {
     G[x][]++;
     G[x][G[x][]]=y;
 }

 int main()
 {
     cin>>N>>M;
     for (int i=;i<=M;i++)
         cin>>dx[i]>>dy[i];

     //1->N:dx[i]->dy[i]走圆内
     //N+1->2*N:dx[i]->dy[i]走圆外
     for (int i=;i<=N;i++)
     {
         for (int j=i+;j<=N;j++)
         {
             if ((dx[j]<dx[i])&&(dx[i]<dy[j])&&(dy[j]<dy[i]))
             {
                 add_edge(i,j+N);
                 add_edge(j+N,i);
                 add_edge(j,i+N);
                 add_edge(i+N,j);
             }
             if ((dx[i]<dx[j])&&(dx[j]<dy[i])&&(dy[i]<dy[j]))
             {
                 add_edge(i,j+N);
                 add_edge(j+N,i);
                 add_edge(j,i+N);
                 add_edge(i+N,j);
             }
         }
     }

     find_scc(*N);

     for (int i=;i<=N;i++)
     {
         if (sccno[i]==sccno[i+N])
         {
             cout<<"the evil panda is lying again"<<endl;
             return ;
         }
     }
     cout<<"panda is telling the truth..."<<endl;
     return ;

 }

------------------------------------------------------------------------------------------------

注意：对于2-SAT问题构图的时候有些题还要纠结一下是连单向边(如poj3678)还是双向边(如本题)，

reference：http://blog.csdn.net/u011026968/article/details/10823853

本题中，我们以第二个判断条件if ((dx[i]<dx[j])&&(dx[j]<dy[i])&&(dy[i]<dy[j]))为例：

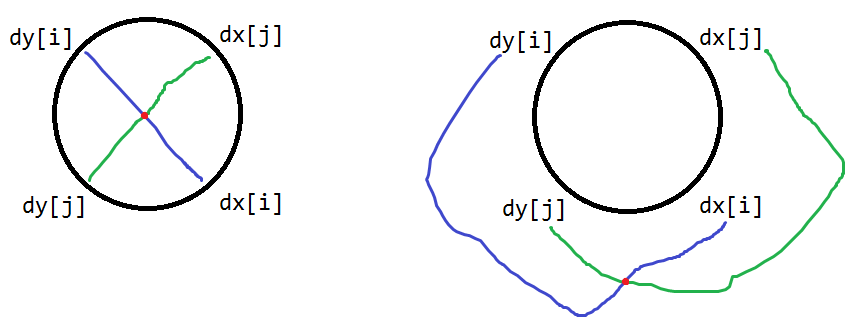
若j在圆内，那么i一定在圆外

若j在圆外，那么i一定在圆内

若i在圆内，那么j一定在圆外

若i在圆外，那么j一定在圆内

注意蓝色部分就是双向边了

------------------------------------

而poj 3683题中：

我们以构图时的第一个判断条件if (min(S[i]+D[i],S[j]+D[j])>max(S[i],S[j]))为例，

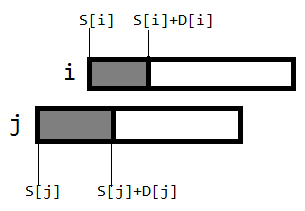
若i在前段举行，那么j一定在后半段举行

若j在后半段举行，那么i不一定要在前半段举行

若j在前段举行，那么i一定在后半段举行

若i在后半段举行，那么j不一定要在前半段举行

注意红色部分：因为不确定（本判断条件中并没有讨论后半段的时间），所以不能双向边