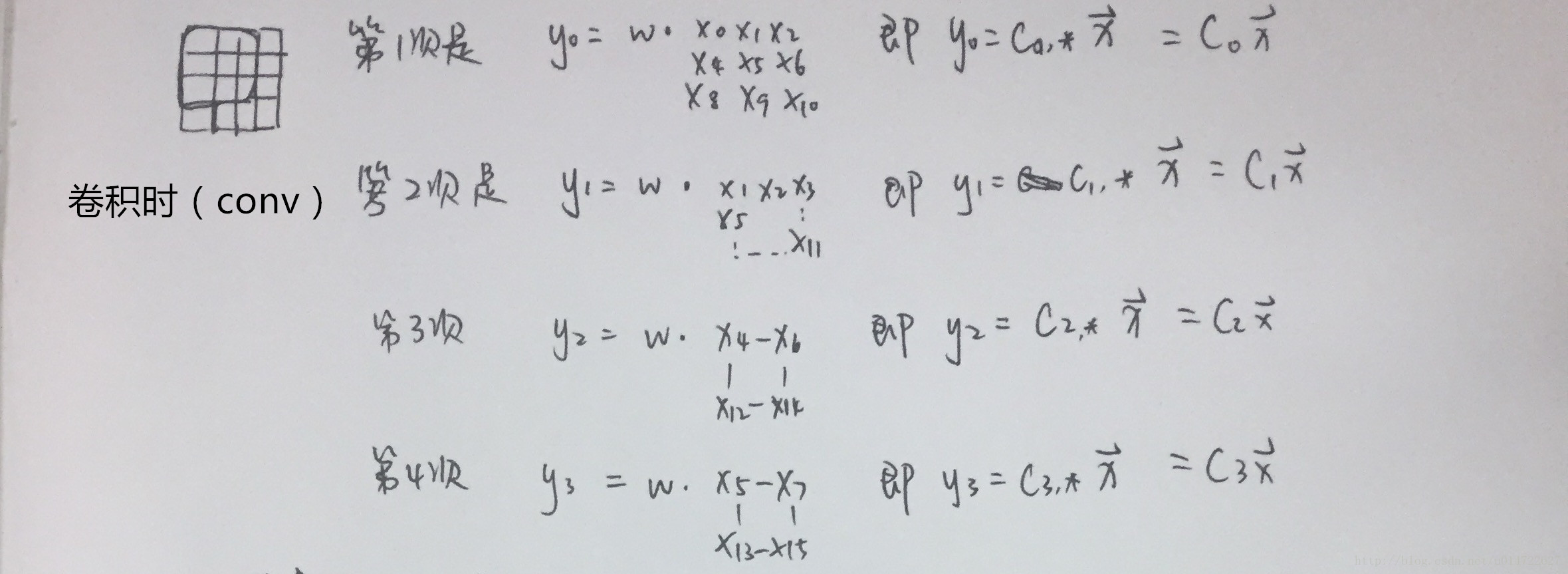深度学习卷积网络中反卷积/转置卷积的理解 transposed conv/deconv
搞明白了卷积网络中所谓deconv到底是个什么东西后,不写下来怕又忘记,根据参考资料,加上我自己的理解,记录在这篇博客里。
先来规范表达
- 为了方便理解,本文出现的举例情况都是2D矩阵卷积,卷积输入和核形状都为正方形,x和y轴方向的padding相同,stride也相同。
- 记号:
i,o,k,p,s i,o,k,p,s 分别表示:卷积/反卷积的输入大小 input size input size,卷积/反卷积输出大小 output size output size,卷积/反卷积核大小 kernel size kernel size, padding padding, stride stride 。 - 举例(如下左图):
输入 X∈R(4,4) X∈R(4,4)矩阵,卷积核 w∈R(3,3),padding=0,stride=1 w∈R(3,3),padding=0,stride=1的情况下,卷积的输出 Y∈R(2,2) Y∈R(2,2),就记为 i=4,o=2,k=3,p=0,s=1 i=4,o=2,k=3,p=0,s=1 。
推翻错误的理解
第一次看到deconv这个词,以为deconv的结果就是卷积的逆,觉得神奇,不禁产生了“哦?转置的卷积就可以求逆了吗?”这样的想法,然后在matlab里面实验求证,我还记得当时以为反卷积能够求逆,考虑到图片进行常规卷积操作输出大小又不可能变大(same/valid),于是我还假设反卷积输出大小不变,用了same padding和原核的转置作为反卷积配置,结果发现根本不是那么一回事好吗。
其实DL中的deconv,是一种上采样过程,举个比方:输入 X∈R(4,4) X∈R(4,4)矩阵,卷积核 w∈R(3,3),pad=0,stride=1 w∈R(3,3),pad=0,stride=1的情况下(如下左图),卷积的输出 Y∈R(2,2) Y∈R(2,2)。对 Y Y进行deconv,它只能做到把还原输出大小到和 X X一样大,输出值和 X X有那么一点联系。
所以啊deconv这个名字相当误导人呐!这在cs231n课程里也被吐槽过,大家现在更喜欢用transposed conv来表述反卷积。为了方便起见,后文就用反卷积这个词了。
第二个容易confused的地方,就是很多文章都说卷积核的转置就可以求反卷积,又陷入迷茫“就算把卷积核转置(或者左右翻转上下翻转),卷积后输出还是越来越小(或不变,至少不会增大)啊”……直到看到文献和相应的这个动画(其他动画在github-convolution arithmetic1)
 |
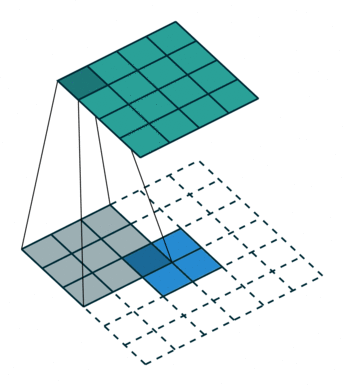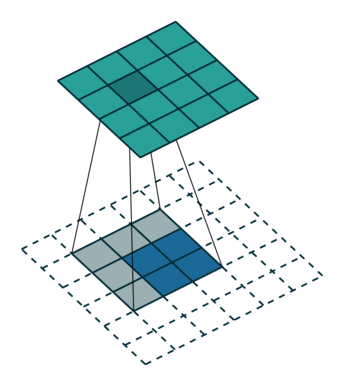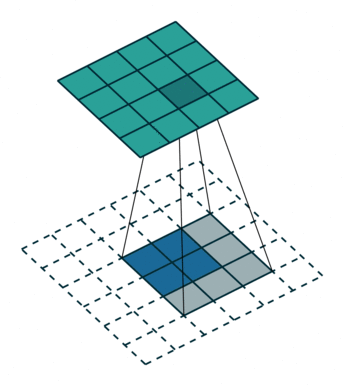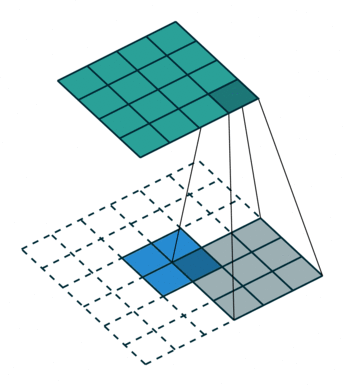 |
|---|---|
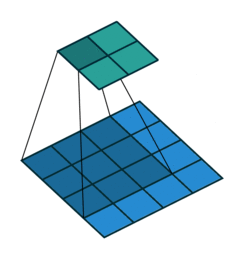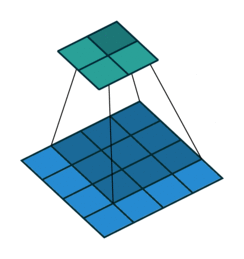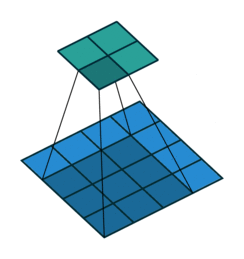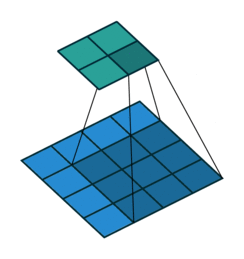
| 卷积 i=4,k=3,p=0,s=1,则 o=2 i=4,k=3,p=0,s=1,则 o=2 | 反卷积 i=2,k=3,p=0,s=1,则 o=4 i=2,k=3,p=0,s=1,则 o=4 |
注意图中蓝色(下面)是输入,绿色(上面)是输出,卷积和反卷积在 p、s、k p、s、k 等参数一样时,是相当于 i i 和 o o 调了个位。
这里说明了反卷积的时候,是有补0的,即使人家管这叫no padding( p=0 p=0),这是因为卷积的时候从蓝色 4×4 4×4 缩小为绿色 2×2 2×2,所以对应的 p=0 p=0 反卷积应该从蓝色 2×2 2×2 扩展成绿色 4×4 4×4。而且转置并不是指这个 3×3 3×3 的核 w w 变为 wT wT,但如果将卷积计算写成矩阵乘法(在程序中,为了提高卷积操作的效率,就可以这么干,比如tensorflow中就是这种实现), Y⃗ =CX⃗ Y→=CX→(其中 Y⃗ Y→ 表示将 Y⃗ Y→ 拉成一维向量, X⃗ X→ 同理),那么反卷积确实可以表示为 CTY⃗ CTY→,而这样的矩阵乘法,恰恰等于 w w 左右翻转再上下翻转后与补0的 Y Y卷积的情况。
然后就产生了第三个confuse:“补0了会不会有影响,还能通过反卷积近似输入 X X 吗?”其实反卷积也不一定能达到近似的效果,图像里的卷积,相当于一种相关操作,而反卷积维持了这种相关操作时的 w w 与 X X、与 Y Y 之间的联系维持了。至于补0后操作是否还等价,上一段已经说明了是等价的,读者可以在阅读完后面的文章后自己尝试一下。
反卷积以及反向传播的过程
卷积和反卷积的过程在arXiv-A guide to convolution arithmetic for deep learning2写的非常详细,还有很多例子便于理解,在这里我就截图出重点来(ps.文中的figure2.1就是上图的左边)。剩下的例子请大家多看看原文,最好自己动手算一下,我也贴个我算的过程( Ci Ci 表示矩阵 C C 的第 i i 行),供参考。
关于反向传播, 知乎-如何理解深度学习中的deconvolution networks3有详细的推导过程。 


深度学习卷积网络中反卷积/转置卷积的理解 transposed conv/deconv的更多相关文章
- CVPR2020:点云分析中三维图形卷积网络中可变形核的学习
CVPR2020:点云分析中三维图形卷积网络中可变形核的学习 Convolution in the Cloud: Learning Deformable Kernels in 3D Graph Con ...
- 吴恩达深度学习笔记(deeplearning.ai)之卷积神经网络(一)
Padding 在卷积操作中,过滤器(又称核)的大小通常为奇数,如3x3,5x5.这样的好处有两点: 在特征图(二维卷积)中就会存在一个中心像素点.有一个中心像素点会十分方便,便于指出过滤器的位置. ...
- 吴恩达深度学习笔记(deeplearning.ai)之卷积神经网络(CNN)(上)
作者:szx_spark 1. Padding 在卷积操作中,过滤器(又称核)的大小通常为奇数,如3x3,5x5.这样的好处有两点: 在特征图(二维卷积)中就会存在一个中心像素点.有一个中心像素点会十 ...
- 卷积网络中的通道(Channel)和特征图
转载自:https://www.jianshu.com/p/bf8749e15566 今天介绍卷积网络中一个很重要的概念,通道(Channel),也有叫特征图(feature map)的. 首先,之前 ...
- 【AI in 美团】深度学习在OCR中的应用
AI(人工智能)技术已经广泛应用于美团的众多业务,从美团App到大众点评App,从外卖到打车出行,从旅游到婚庆亲子,美团数百名最优秀的算法工程师正致力于将AI技术应用于搜索.推荐.广告.风控.智能调度 ...
- 【腾讯Bugly干货分享】深度学习在OCR中的应用
本文来自于腾讯bugly开发者社区,未经作者同意,请勿转载,原文地址:http://dev.qq.com/topic/5809bb47cc5e52161640c5c8 Dev Club 是一个交流移动 ...
- 【深度学习】CNN 中 1x1 卷积核的作用
[深度学习]CNN 中 1x1 卷积核的作用 最近研究 GoogLeNet 和 VGG 神经网络结构的时候,都看见了它们在某些层有采取 1x1 作为卷积核,起初的时候,对这个做法很是迷惑,这是因为之前 ...
- Attention机制在深度学习推荐算法中的应用(转载)
AFM:Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Ne ...
- 深度学习训练过程中的学习率衰减策略及pytorch实现
学习率是深度学习中的一个重要超参数,选择合适的学习率能够帮助模型更好地收敛. 本文主要介绍深度学习训练过程中的6种学习率衰减策略以及相应的Pytorch实现. 1. StepLR 按固定的训练epoc ...
随机推荐
- Django之ORM字段和字段参数
ORM介绍 ORM概念 ORM由来 ORM的优势 ORM的劣势 ORM总结 Django中的ORM Django项目使用MySQL数据库 Model 快速入门 字段 自定义字段 字段参数 Model ...
- 关于java.lang.ClassCastException: [Ljava.lang.Object; cannot be cast to 实体类
由于业务逻辑的复杂,有些sql语句写法hql不支持,所以hibernate查询直接用了sql原生查询,由于数据结果根据四个表查询出来,所以无法使用方法.addEntity(XXXXXXX.class) ...
- JavaScript基础笔记(十三)测试和调试
错误处理与测试 一.错误处理 一)try-catch语句 function atest() { try { //可能发生错误的代码 return 0; } catch (error) { //错误处理 ...
- 潭州课堂25班:Ph201805201 tornado 项目 第一课 项目介绍和创建 (课堂笔记)
tornado 相关说明 , 查找 python3 的路径: binbin@abc:~$ which python3/usr/bin/python3 创建虚拟环境 : 创建工程; 用 pycharm ...
- 哈希表(散列表),Hash表漫谈
1.序 该篇分别讲了散列表的引出.散列函数的设计.处理冲突的方法.并给出一段简单的示例代码. 2.散列表的引出 给定一个关键字集合U={0,1......m-1},总共有不大于m个元素.如果m不是很大 ...
- Springboot2.x 启动报错:Bean named 'xxxService'... but was actually of type 'com.sun.proxy.$Proxy82'
Springboot 2.0.5 搭建一个新项目启动后报错:Bean named 'xxxService'... but was actually of type 'com.sun.proxy.$Pr ...
- LINUX文件及目录管理命令基础(2)
Linux文件类型 文件作为Linux操作系统中最常见的对象,在系统中被分为了多种类型 如下: - 普通文件 d 目录 l 链接 b 块设备 c 字符设备 p 管道设备 s 套接字文件 Linux目录 ...
- C Windows控制台字符版本俄罗斯方块
//一个可以工作在Windows控制台字符界面下的俄罗斯方块 //工作在非图形模式,无需其他库依赖,单个C文件代码即可运行 //支持最高纪录,并且对于纪录进行了加密 //By wrule 2015年1 ...
- phpstorm连接ftp
1.先到服务器中添加一个专门连接ftp的账号 useradd --help useradd -c sftp -d /data/project/testdir/ -g root -M sftp // 创 ...
- Java 不变模式
在阎宏博士的<JAVA与模式>一书中开头是这样描述不变(Immutable)模式的:一个对象的状态在对象被创建之后就不再变化,这就是所谓的不变模式. 不变模式的结构 不变模式可增强对象的健 ...