POJ-图论-并查集模板

POJ-图论-并查集模板

1、init：把每一个元素初始化为一个集合，初始化后每一个元素的父亲节点是它本身，每一个元素的祖先节点也是它本身（也可以根据情况而变）。

void init()
{
    for (int i = 0; i < n; i++) p[i] = i;//p[i]即为i结点的父亲节点的编号
}

2、find(x) ：查找一个元素所在的集合，即找到这个元素所在集合的祖先，判断两个元素是否属于同一集合，只要看他们所在集合的祖先是否相同即可。合并两个集合，也是使一个集合的祖先成为另一个集合的祖先。

int find(int x)
{
    return x == p[x] ? x : p[x] = find(p[x]);//已包含路径压缩
}

3、Union(x,y) ：合并x,y所在的两个集合，利用find()找到其中两个集合的祖先，将一个集合的祖先指向另一个集合的祖先。如图

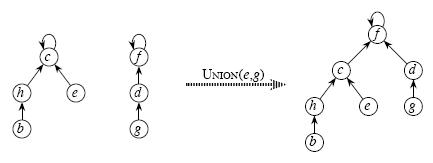
void Union(int x, int y)
{
    x = find(x);
    y = find(y);

    if (x == y) return;
    else p[y] = x;//把y树合并到x树上，以x为根
}

POJ 2524 Ubiquitous Religions

解题思路

并查集入门题，求出有多少个不同的连通分量即可。

AC代码

#include<cstdio>
const int N = ;

int p[N];//父结点数组
int n, m;//结点数量和结点关系数量

void init()
{
    for (int i = ; i < n; i++)p[i] = i;//初始化，父结点为自身，单结点为孤立树
}

int find(int x)//找到x所在树的根结点
{
    return (x == p[x]) ? x : p[x] = find(p[x]);
}

void Union(int x, int y)//合并，将y树合并到x树上
{
    x = find(x);
    y = find(y);
    if (x == y)return;
    else p[y] = x;
}

int main()
{
    int cnt = ;
    while (scanf("%d%d", &n, &m)!=EOF)
    {
        if (n ==  && m == ) break;
        int x, y;
        init();//初始化，清空数组
        for (int i = ; i < m; i++)
        {
            scanf("%d%d", &x, &y);
            Union(x, y);
        }
        int ans = ;
        for (int i = ; i < n; i++)
        {
            if (i == p[i])ans++;
        }
        printf("Case %d: %d\n", cnt++, ans);
    }
    return ;
}

POJ 1611 The Suspects

解题思路

至于一个小组有多个人，从第二个人起与第一个人所在小组合并就好。

AC代码

#include<cstdio>
const int N = ;

int p[N];//父结点数组
int n, m;//结点数量和结点关系数量

void init()
{
    for (int i = ; i < n; i++)p[i] = i;//初始化，父结点为自身，单结点为孤立树
}

int find(int x)//找到x所在树的根结点
{
    return (x == p[x]) ? x : p[x] = find(p[x]);
}

void Union(int x, int y)//合并，将y树合并到x树上
{
    x = find(x);
    y = find(y);
    if (x == y)return;
    else p[y] = x;
}

int main()
{
    while (scanf("%d%d", &n, &m)!=EOF)
    {
        if (n ==  && m == ) break;
        int groupNum, x, y;
        init();//初始化，清空数组
        while(m--)
        {
            scanf("%d%d", &groupNum, &x);
            while (--groupNum)
            {
                scanf("%d", &y);
                Union(x, y);//每个组员与第一个组员所在团体合并
            }
        }
        int ans = ;
        for (int i = ; i < n; i++)//自己也是患者
        {
            if (find(i) == find())ans++;//和0号有关系的学生
        }
        printf("%d\n", ans);
    }
    return ;
}