LibreOJ #525. 「LibreOJ β Round #4」多项式

二次联通门 : LibreOJ #525. 「LibreOJ β Round #4」多项式

官方题解 :

/*
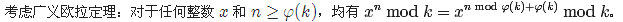
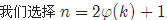
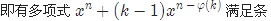
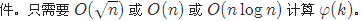
    LibreOJ #525. 「LibreOJ β Round #4」多项式

    由于会有多种解
    所以只需要找出一组特殊解即可

*/
#include <cstdio>
#include <iostream>

void read (int &now)
{
    register char c = getchar ();
    for (now = ; !isdigit (c); c = getchar ());
    for (; isdigit (c); now = now *  + c - '', c = getchar ());
}

int Main ()
{
    int N; read (N); register int i, j; int L = N;
    int phi = ; if (N == ) return printf ("-1"), ;
    for (i = ; i * i <= L; ++ i)
        if (L % i == )
        {
            L /= i, phi *= (i - );
            for (; L % i == ; L /= i, phi *= i);
        }
    if (L != ) phi *= L - ;
     printf ("%d\n", L = phi <<  | ); ++ phi;
    for (i = ; i < phi; ++ i) printf ("0 ");
    printf ("%d ", N - );
    for (++ i; i < L; ++ i) printf ("0 ");
    printf ("");
    return ;
}

int ZlycerQan = Main ();
int main (int argc, char *argv[]) {;}