Bias vs. Variance(3)---用learning curves来判断bias/variance problem

画learning curves可以用来检查我们的学习算法运行是否正常或者用来改进我们的算法，我们经常使用learning cruves来判断我们的算法是否存在bias problem/variance problem或者两者皆有。

learning curves--m(trainning size与error的函数)

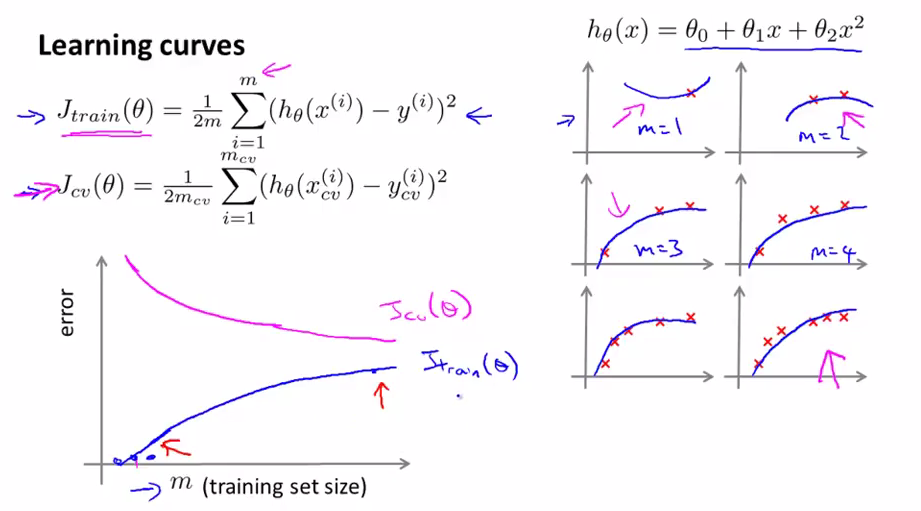
上图是J_train(θ)与J_cv(θ)与training set size m的关系图，假设我们使用二次项来拟合我们的trainning data。

当trainning data只有一个时，我们能很好的拟合，即J_train(θ)=0;当trainning data有二个时，我们也能很好的拟合，即J_train(θ)=0；随着training data set数量的增加，J_train(θ)也递增；

当trainning data很小时，预测函数的泛化(generalization)就很弱,所以J_cv(θ)就很大，随着raining data set数量的增加，泛化能力增强(对新样本的适应能力增强)，J_cv(θ)递减。

learning curves with high bias--增加training data是没有用的

当我们要用一条直线来模拟上图中的数据时，hypothesis处于high bias的情况，如上图所示，我们有5个样本点是，直线是那样的，我们将样本点增加到10个，直线还是那样的，不会因为我们增加了样本的个数会对数据模拟得更好，所以对于处于high bias的算法，我们增加training data是没有用的。

在high bias的情况下，刚开始样本点少时，J_train(θ)很小，随着样本点越来越多，hypothesis不能拟合太多的样本(underfit状态)，J_train(θ)越来越大

在high bias的情况下，刚开始样本点少时，J_cv(θ)很大(因为少的样本点缺乏泛化能力)，随着样本点的增多，J_cv(θ)变小，小到一个值就会趋于平缓(相对还是很大的值),即不会对我们hypothesis发生什么改变。

在high bias的情况下，J_train(θ)和J_cv(θ)随着样本的增大趋于相近的值(high error)

learning curves with high variance--增加training data是有帮助的

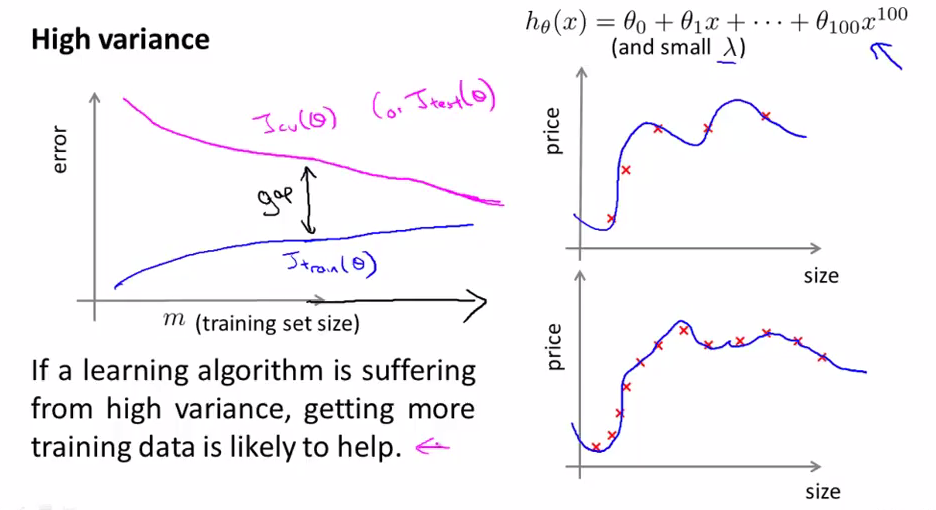
当我们的算法处于high variance情况下，如上图所示x有100次方(假设的情况)并且λ 值很小，这时我们的hypothesis处于high variance.

对于只有5个trainning data的情况，我们的hypothesis能拟合得很好，即当training set size小时，J_train(θ)也很小，随着training set size的增加，hypothesis不会每个点都拟合了，这时J_train(θ)会有所上升，但还是比较小的；

对于只有5个trainning data的情况，我们出现了overfitting的现象，这时J_cv(θ)很大，随着样本的增多，我们的泛化能力增强，J_cv(θ)下降，但是与J_train(θ)有一段gap(表明J_cv(θ)>>J_train(θ),overfitting的表现)，这时如果我们延伸m，即扩大training set size,J_train(θ)上升，J_cv(θ)下降，如上图所示。所以增加training data是有帮助的。

上述两种情况下的learning curve都是理想情况下的，实际情况会有些不同(可能会有些噪声和干扰的曲线)，但是会出现基本类似的结果，可以帮助我们看清我们的学习算法是否处于high bias/high variance/or both。所以当我们想要改进一个学习算法的性能时，我们通常都会画出learning curve,可以让我们更加看清bias or variance problem