CFGym 101490E 题解

一、题目链接

　　http://codeforces.com/gym/101490

二、题面

　　

三、题意

　　给你一个图，n个点，m条边，一个x，从顶点1走到顶点n。假设从顶点1走到顶点n的最短路为d，x代表你可以选择的路径的长度范围：[d, d * (1 + x%)]。让你求出在所有长度在此区间内的路径，路径上最大的边的最小值。如图所示：

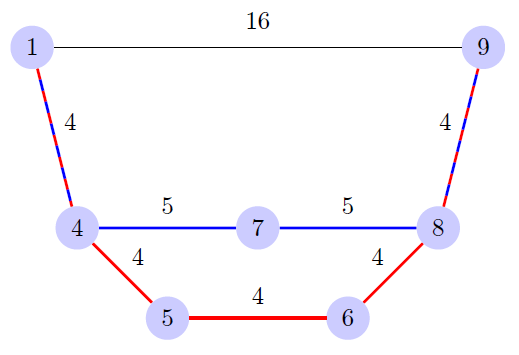
　　从顶点1到顶点9的最短距离为16。所以，可选的路径范围是：[16, 18.4]。可以发现，1->4->7->8->9这条路径的长度为18，是在此区间内的，而且这条路径上的边最大值为5。而另一条有效路径是1->9，边最大值是16。所以，答案是5。

四、思路

　　先跑一遍最短路算法，得到从顶点1到顶点n的最短路径。然后，二分最大边权，把大于枚举值mid的边全部删掉，再跑最短路，如果从1到n的最短路在[d, d * (1 + x%)]范围内，说明枚举的mid是有效的。最后输出枚举的最小的最大值即可。

　　删边怎么删呢？千万别用set或者vector之类的容器去模拟删除，这样复杂度会大很多。快速的方法是：使用两个图，一个是原图，另一个是二分最大边权的图，每次枚举一个mid时，都用原图来筛选，把大于mid的边直接过滤掉就OK了。

　　为什么这样是正确的呢？因为答案是满足单调性的。（现在我只能这么写。有些感觉上的东西实在是表达不出来呀。）

五、源代码

　　

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, LL> PLL;//first:邻接点，second:和邻接点之间的边权。
;
vector<PLL> g[][MAXN];
int n, m, x;
double minl, maxl;
typedef pair<LL, int> P;//跑dijstra算法必备的。
LL d[MAXN];

LL djst(int s, int which) {
    priority_queue<P, vector<P>, greater<P> > que;
    memset(d, 0x3f, sizeof(d));
    d[s] = ;
    que.push(P(, s));
    while(!que.empty()) {
        P p = que.top();
        que.pop();
        int v = p.second;
        if(d[v] < p.first)continue;
        , sz = g[which][v].size(); i < sz; ++i) {
            PLL pll = g[which][v][i];
            if(d[pll.first] > d[v] + pll.second) {
                d[pll.first] = d[v] + pll.second;
                que.push(P(d[pll.first], pll.first));
            }
        }
    }
    return d[n];
}

bool test(LL mid){
    ;i < MAXN;++i)g[][i].clear();
    ;i <= n;++i){
        , sz = g[][i].size();j < sz;++j){
            PLL pll = g[][i][j];
            ][i].push_back(pll);
        }
    }
    LL dis = djst(, );
    double ddis = (double)dis;
    if(ddis > minl && ddis < maxl)return true;
     || fabs(ddis - maxl) < 1e-)return true;
    return false;
}

int main() {
#ifndef ONLINE_JUDGE
    freopen("Einput.txt", "r", stdin);
#endif // ONLINE_JUDGE
    int a, b;
    LL c;
    while(~scanf("%d%d%d", &n, &m, &x)) {
        ; i < MAXN; ++i)g[][i].clear();
        ; i <= m; ++i) {
            scanf("%d%d%lld", &a, &b, &c);
            g[][a].push_back(make_pair(b, c));
            g[][b].push_back(make_pair(a, c));
        }
        minl = (, );
        maxl = minl * (1.0 + x * 1.0 / 100.0);
        LL low = -, high = 1LL << , mid;
        ){
            mid = (low + high) / ;
            if(test(mid))high = mid;
            else low = mid;
        }
        printf("%lld\n", high);
    }
    ;
}

 经验：long long类型的数值做数组下标也是没问题的。这样，在需要使用long long数据类型的题目中，通通使用long long数据类型，包括for循环，这样可以省去各种麻烦的类型转换操作。尤其是使用C/C++语言，编译器没有自动类型转换的情况下。