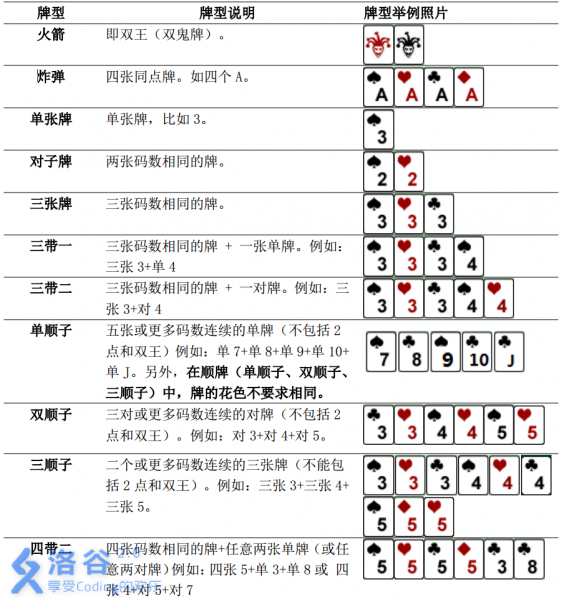
NOIP2015提高组D1T3 斗地主

问一副排n张，n<=23最少打几次打完，数据组数T<=100。

面向数据编程。。

前30分：乱暴力？没有顺子，把单、对子、炸弹、三张、王炸、三带一判一次即可。

前70分：状压，先预处理哪些状态能一次出完，用这些状态来转移，2^n*n*T。实际得分可能比期望的高一些？？

满分：如果不打顺子，最优策略是可以确定的，三和四的能带走一二的就带走。所以dfs打顺子，然后贪心出剩下的牌。可以把ans做全局变量，然后搜索时>ans就退出以剪枝。

 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 //#include<assert.h>
 //#include<time.h>
 #include<math.h>
 //#include<queue>
 #include<algorithm>
 #include<iostream>
 using namespace std;

 bool isdigit(char c) {return c>='' && c<='';}
 int qread()
 {
     char c;int s=,f=;while (!isdigit(c=getchar())) f=(c=='-'?-:);
     do s=s*+c-''; while (isdigit(c=getchar())); return s*f;
 }

 int T,n,ans;
 int a[],cnt[];
 int calc()
 {
     int ans=;
     memset(cnt,,sizeof(cnt));
     for (int i=;i<=;i++) cnt[a[i]]++;
     for (int i=;i<=;i++) cout<<cnt[i]<<' ';cout<<endl;
     bool wang=;
     if (a[] && a[]) cnt[]++,wang=;
     else if (a[] || a[]) cnt[]++;else{}

     while (cnt[] && cnt[]>) ans++,cnt[]--,cnt[]-=;
     while (cnt[] && cnt[]>) ans++,cnt[]--,cnt[]-=;
     while (cnt[] && cnt[]) ans++,cnt[]--,cnt[]--;
     while (cnt[] && cnt[])
     {
         if (cnt[]== && wang) break;
         ans++,cnt[]--,cnt[]--;
     }
     ans+=cnt[]+cnt[]+cnt[]+cnt[];
     return ans;
 }
 void dfs(int dep)
 {
     if (dep>ans) return;
     int tmp=calc();
     if (dep+tmp<ans) ans=dep+tmp;
     //单顺子
     for (int i=;i<=;i++)
     {
         int j=i;
         while (j< && a[j]) j++;
         for (int play=i+;play<j;play++)
         {
             for (int k=i;k<=play;k++) a[k]--;
             dfs(dep+);
             for (int k=i;k<=play;k++) a[k]++;
         }
     }
     //连对
     for (int i=;i<=;i++)
     {
         int j=i;
         while (j< && a[j]>) j++;
         for (int play=i+;play<j;play++)
         {
             for (int k=i;k<=play;k++) a[k]-=;
             dfs(dep+);
             for (int k=i;k<=play;k++) a[k]+=;
         }
     }
     //三连对
     for (int i=;i<=;i++)
     {
         int j=i;
         while (j< && a[j]>) j++;
         for (int play=i+;play<j;play++)
         {
             for (int k=i;k<=play;k++) a[k]-=;
             dfs(dep+);
             for (int k=i;k<=play;k++) a[k]+=;
         }
     }
 }
 int main()
 {
     T=qread();
     n=qread();
     int x,y;
 while (T--)
 {
     memset(a,,sizeof(a));
     for (int i=;i<=n;i++)
     {
         x=qread();y=qread();
         if (x)
         {
             if (x>) a[x-]++;
             else a[x+]++;
         }
         else a[+y]++;
     }
     ans=n;dfs();
     printf("%d\n",ans);
 }
     return ;
 }

错误！有诸多未考虑到的情况，比如，4张3，4张3，3张5，可以两次打完；4张3，3张4，3张5，2张6，也可以两次打完。。。

不过这样可以满足网上大部分的数据了。。