【2018.10.15】noip模拟赛Day1

题面

wzj的题解

T1

随便搜

 #include<bits/stdc++.h>
 #define ll long long
 using namespace std;
 inline int read(){
     int x=; bool f=; char c=getchar();
     for(;!isdigit(c);c=getchar()) if(c=='-') f=;
     for(; isdigit(c);c=getchar()) x=(x<<)+(x<<)+(c^'');
     if(f) return x;
     return -x;
 }
 int T,len;
 char c[];
 ll L;
 bool dfs2(int wz,ll cur,ll sum,bool Last){
     if(!(wz^len)) return sum+cur==L ?  : ;
     if(Last== && dfs2(wz,,sum+cur,)) return ;
     if(dfs2(wz+,(cur<<)+(cur<<)+(c[wz]^''),sum,)) return ;
     return ;
 }
 bool dfs(int wz,ll cur,ll sum,bool Last){
     if(!(wz^len)) return ;
     if(Last==){
         L=sum+cur;
         if(dfs2(wz,,,)) return ;
     }
     if(Last== && dfs(wz,,sum+cur,)) return ;
     if(dfs(wz+,(cur<<)+(cur<<)+(c[wz]^''),sum,)) return ;
     return ;
 }
 int main(){
     T=read();
     while(T--){
         scanf("%s",c);
         len=strlen(c);
         if(dfs(,,,)) printf("Yes\n");
         else printf("No\n");
     }
     return ;
 }

T2

一道奇怪的题目。

首先想想dp，不好想。于是推推结论。

很快发现交换两个数只与以这两个数为两端的区间有关系。

具体就是说

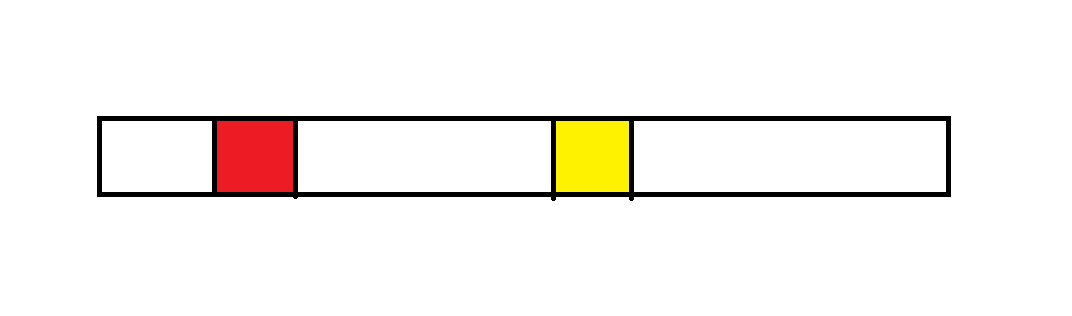
你交换红黄两个位置的数，跟红块左边和黄块右边的部分是没有关系的，因为这两块中的0/1与外部的0/1的相对位置没变。

然后还会发现对于交换的两个数，只有左边是0、右边是1时才有意义，否则可以发现逆序对数不会多，花费也不会少，肯定不优。

然后左边的0和右边的1交换会增加多少逆序对呢？假设交换的两数的坐标分别为$i,j$，考虑两数中间部分$(i,j)$的取值。

对于中间所有的0，把1换到前面后它们会各自和前面的1形成一组新的逆序对；

对于中间所有的1，把0换到后面后它们会各自和后面的0形成一组新的逆序对。

也就是说，中间部分有多少个数，两端交换后就会出现多少新的逆序对。

再加上交换的一对0和1又形成一组新的逆序对，一次交换会形成$j-i$组新的逆序对。

将它和花费$cost_i+cost_j$作差，就得到了对答案的贡献。

显然，一组交换对答案的贡献 $\le 0$ 的话肯定不如不换。

那如果一组交换对答案的贡献 $\gt 0$，交换后一定更优么？

我们就得考虑交换结果与交换的先后顺序是否有关了。

首先，交换一组数肯定需要$cost_i+cost_j$的花费，有经验的同学会直观感觉这样的交换与先后顺序无关。

那怎么验证呢？我们取$2$组交换的情况即可。

1.两组交换区间不相交

T3

一眼认数据结构，两眼认线段树，三眼认树状数组。

一看区间操作机器人位置，那不就是线段树维护每个机器人的坐标了……

对于1操作，相当于区间赋值，打位置$tag_w$并打个清空子树中所有记录向父亲移动步数的$tag_f$的标记（因为后赋值刷掉前面的移动）。

对于2操作，跟1差不多，打向父亲移动步数的$tag_f$。

对于3操作，首先单点查询（查询一个机器人的当前位置），查到那个点的时候，先判断是否要用$tag_w$更新当前机器人在上一次1操作移到的位置，再将其向父亲移动$tag_f$步。

　　　　　  其次要维护一个子树和。我们可以按dfs序开两个树状数组分别表示 子树所有点的权值和 & 子树内有多少个开灯的点。（其中一个点的权值就是它的深度，它减去另一个点的深度就是两点的距离咯）。