多边形面积(Area_Of_Polygons)

原理：

任意多边形的面积可由任意一点与多边形上依次两点连线构成的三角形矢量面积求和得出。

分析： 
由于给出的点是相对于我们的坐标原点的坐标，每个点实际上我们可以当作一个顶点相对于原点的向量，如下图所示：

 
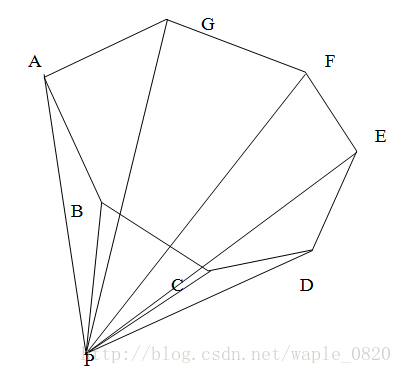
P(0,0)对应的顶点向量分别为：A(x0,y0),B(x1,y1),…,G(x6,y6) 
另外，△PAB△PAB的矢量面积即为

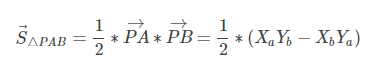
且多边形面积为：

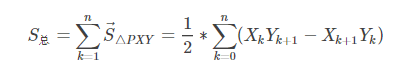
根据上述公式可以直接求出多边形的代码从而避免了边长的复杂计算。

例题：

https://ac.nowcoder.com/acm/contest/328/F

题解：计算几何裸题

#include <bits/stdc++.h>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<string>
#include<vector>
#include<bitset>
#include<queue>
#include<deque>
#include<stack>
#include<cmath>
#include<list>
#include<map>
#include<set>
//#define DEBUG
#define RI register int
using namespace std;
typedef long long ll;
//typedef __int128 lll;
const int N=+;
const int MOD=1e9+;
const double PI = acos(-1.0);
const double EXP = 1E-;
const int INF = 0x3f3f3f3f;
int t,n,m,k,q;
double ans;
struct node{
    double x,y;

}e[N];
double a[N];
char str;
int main()
{
#ifdef DEBUG
    freopen("input.in", "r", stdin);
    //freopen("output.out", "w", stdout);
#endif
    scanf("%d%d",&n,&q);
    if(n==){
        printf("%.6f",ans);
        return ;
    }
    for(int i=;i<=n;i++){
        scanf("%lf%lf",&e[i].x,&e[i].y);
    }
    for(int i=;i<=n;i++){
        if(n==)
        a[i]=a[i-]+e[i].y*e[n].x-e[i].x*e[n].y;
        else
        a[i]=a[i-]+e[i].y*e[i-].x-e[i].x*e[i-].y;
    }
    double sum=fabs(a[n]/);
    //cout<<sum<<endl;
    int s,t;
    while(q--){
        scanf("%d%d",&s,&t);

        if(s>t)
            swap(s,t);
        if(abs(s-t)==||s==&&t==n)
            continue;
        double sumtmp=fabs((a[t]-a[s]+e[s].y*e[t].x-e[s].x*e[t].y)/);
        ans=max(ans,min(sumtmp,sum-sumtmp));
    }
    printf("%.6f",ans);
    //cout << "Hello world!" << endl;
    return ;
}

C++版本二

题解：

计算几何
只要叉积维护一下前缀和就好了。

#include <cstdio>
#include <bits/stdc++.h>
#include <map>
#include <cstring>
#include <algorithm>
using namespace std;
#define mst(a,b) memset((a),(b),sizeof(a))
#define rush() int T;scanf("%d",&T);while(T--)

typedef long long ll;
const int maxn = ;
const ll INF = 1e18;
const ll mod=1e9+;
const double eps = 1e-;

int n,m;

struct node
{
    double x,y;
}a[maxn];

double sum[maxn];

double cross(node a,node b,node c)
{
    return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)
    {
        scanf("%lf%lf",&a[i].x,&a[i].y);
    }
    node zero;
    zero.x=;
    zero.y=;
    for(int i=;i<=n;i++)
    {
        double ans=cross(zero,a[i],a[(i==n?:i+)]);
        sum[i]=sum[i-]+ans;
    }
    for(int i=n+;i<=*n;i++)
    {
        sum[i]=sum[i-]+sum[i-n];
    }
    double Sum=fabs(sum[n])/2.0;
    double cnt=;
    for(int i=;i<m;i++)
    {
        int ss,tt;
        scanf("%d%d",&ss,&tt);
        if(ss>tt) swap(ss,tt);
        double ans=sum[tt-]-sum[ss-];
        ans+=cross(zero,a[tt],a[ss]);
        ans=fabs(ans)/2.0;
        cnt=max(cnt,min(ans,Sum-ans));
    }
    printf("%.15f\n",cnt);
}