这是我们课程的服务里面 加了授权的方法

重启课程管理的服务

首先需要登陆

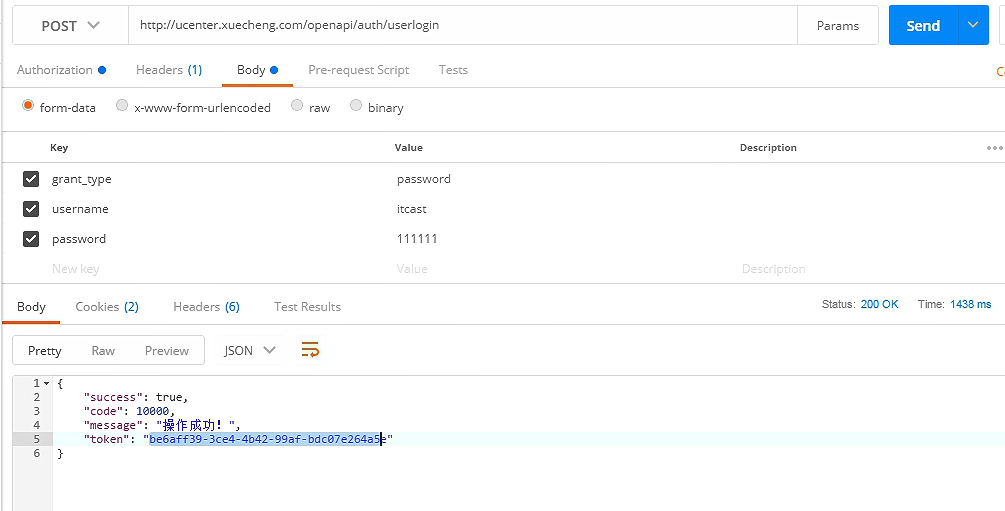
在redis复制token

访问课程列表


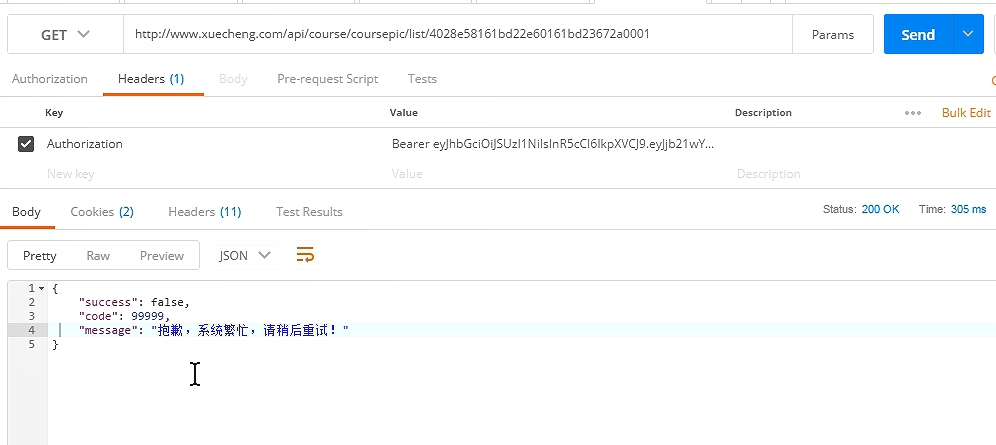
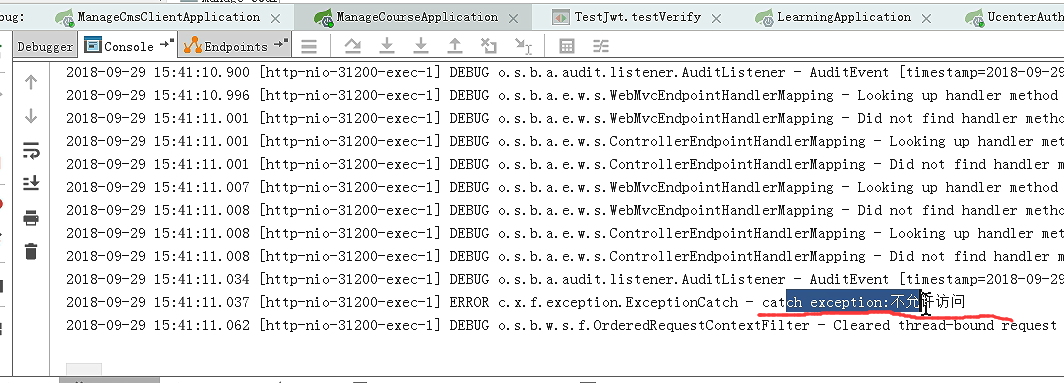
用最新复制的令牌

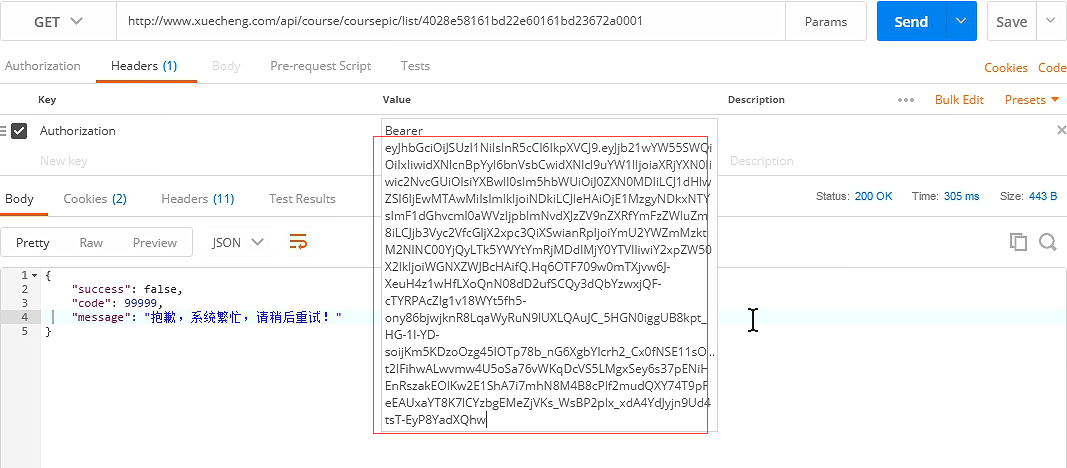
最新token可以

调用teachplan方法

调用 一个没加注解的方法

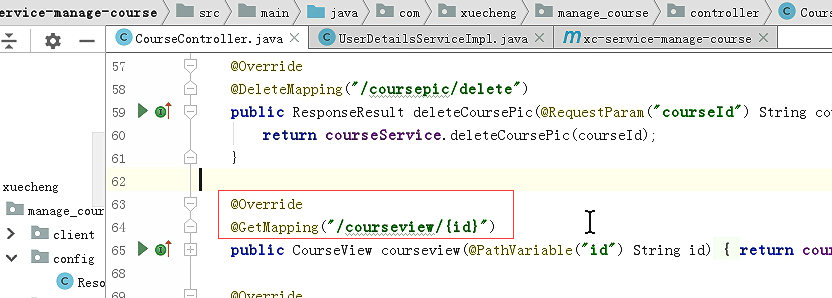
所以肯定可以访问

结束

阶段5 3.微服务项目【学成在线】_day18 用户授权_05-方法授权-方法授权测试的更多相关文章

  1. 阶段5 3.微服务项目【学成在线】_day04 页面静态化_16-页面静态化-模板管理-模板制作

    这是轮播图的原始文件 运行门户需要把 nginx启动起来 单独运行轮播图.把里面的css的引用都加上网址的url 这就是单独访问到的轮播图的效果 轮播图模板的地址: 阶段5 3.微服务项目[学成在线] ...

  2. 阶段5 3.微服务项目【学成在线】_day02 CMS前端开发_16-CMS前端工程创建-导入系统管理前端工程

    提供了基于脚手架封装好的前端工程 H:\BaiDu\黑马传智JavaEE57期 2019最新基础+就业+在职加薪\阶段5 3.微服务项目[学成在线]·\day02 CMS前端开发\资料\xc-ui-p ...

  3. 阶段5 3.微服务项目【学成在线】_day16 Spring Security Oauth2_03-用户认证技术方案-Oauth2协议

    2.2 Oauth2认证 2.2.1 Oauth2认证流程 第三方认证技术方案最主要是解决认证协议的通用标准 问题,因为要实现 跨系统认证,各系统之间要遵循一定的 接口协议. OAUTH协议为用户资源 ...

  4. 阶段5 3.微服务项目【学成在线】_day16 Spring Security Oauth2_01-用户认证需求分析

    1.1 用户认证与授权 截至目前,项目已经完成了在线学习功能,用户通过在线学习页面点播视频进行学习.如何去记录学生的学习过程 呢?要想掌握学生的学习情况就需要知道用户的身份信息,记录哪个用户在什么时间 ...

  5. 阶段5 3.微服务项目【学成在线】_day09 课程预览 Eureka Feign_05-Feign远程调用-客户端负载均衡介绍

    2 Feign远程调用 在前后端分离架构中,服务层被拆分成了很多的微服务,服务与服务之间难免发生交互,比如:课程发布需要调用 CMS服务生成课程静态化页面,本节研究微服务远程调用所使用的技术. 下图是 ...

  6. 阶段5 3.微服务项目【学成在线】_day09 课程预览 Eureka Feign_02-Eureka注册中心-搭建Eureka单机环境

    我们先搭建单机环境 govern是治理的意思, 这样就把工程创建好了 创建包 创建SpringBoot的启动类. 在父工程里面已经确定了Spring Cloud的版本了.相当于锁定了版本 接下里只需要 ...

  7. 阶段5 3.微服务项目【学成在线】_day09 课程预览 Eureka Feign_04-Eureka注册中心-将服务注册到Eureka Server

    cms相当于客户端 配置客户端的信息 后面加逗号分隔开 50102表示向两台eureka服务上报服务,如果有一台死掉了 那么还可以上另外的一台去注册服务 直接把ip注册到eureka 启动类加注解 重 ...

  8. 阶段5 3.微服务项目【学成在线】_day09 课程预览 Eureka Feign_01-Eureka注册中心-Eureka介绍

    1 Eureka注册中心 1.1 需求分析 在前后端分离架构中,服务层被拆分成了很多的微服务,微服务的信息如何管理?Spring Cloud中提供服务注册中 心来管理微服务信息. 为什么 要用注册中心 ...

  9. 阶段5 3.微服务项目【学成在线】_day18 用户授权_03-方法授权-jwt令牌包含权限

    修改认证服务的UserDetailServiceImpl类,下边的代码中 permissionList列表中存放了用户的权限, 并且将权限标识按照中间使用逗号分隔的语法组成一个字符串,最终提供给Spr ...

  10. 阶段5 3.微服务项目【学成在线】_day17 用户认证 Zuul_14-网关-介绍网关及搭建网关工程

    4 Zuul网关 4.1 需求分析 网关的作用相当于一个过虑器.拦截器,它可以拦截多个系统的请求. 本章节要使用网关校验用户的身份是否合法. 4.2 Zuul介绍 什么是Zuul? Spring Cl ...

随机推荐

  1. MySQL进阶18- 存储过程- 创建语句-参数模式(in/out/inout-对应三个例子) -调用语法-delimiter 结束标记'$'- 删除/查看/修改-三个练习

    /* MySQL-进阶18 存储过程 和 函数 存储过程和函数:类似于java中的方法 好处: 1.提高代码的重用性 2.简化操作 */ #存储过程 /* 含义: 一组已经预见编译好的SQL语句的集合 ...

  2. CentOS7.x安装mariadb-10.3

    1.配置mariadb yum源 vim /etc/yum.repos.d/mariadb.repo # 写入如下内容 [mariadb] name = MariaDB baseurl = http: ...

  3. vscode 输出面板字符编码问题

    默认的输出中文会显示成乱码,需要在vscode内部的终端中输入 chcp 65001 缺点是需要每次打开vscode进行激活,另一种方式是在vscode的首选项中进行配置: "termina ...

  4. JSP中9大内置对象类型

    JSP中九大内置对象为: request            请求对象                 类型 javax.servlet.ServletRequest        作用域 Requ ...

  5. eclipse/myeclipse SVN资源库URL中文乱码问题解决办法

    右击选择资源库地址 可以自定义名称

  6. myeclipse2018修改主题

  7. [Codevs] 一塔湖图

    http://codevs.cn/problem/1024/ floyd 走起 #include <iostream> #include <cstdio> #include & ...

  8. [cogs] 传染病控制

    http://cogs.pro:8080/cogs/problem/problem.php?pid=107 去年6月份的代码了,又长又臭又WA 暴力贪心模拟 水水50 #include<iost ...

  9. Zotero使用教程(1)-安装及配置

    小书匠kindle   作为一名科研人员,经常要阅读大量文献(当然我收集>>阅读,哎!),收集来的文献一般我们使用文件夹管理,通常使用文件夹命名和层级分布解决论文的分类问题.   但是,实 ...

  10. 数据结构实验之图论十：判断给定图是否存在合法拓扑序列（SDUT 2140）

    分析:BFS判断是否有环. #include<bits/stdc++.h> using namespace std; typedef long long ll; int gra[200][ ...