luoguP3373 【模板】线段树 2

P3373 【模板】线段树 2

• • 969通过
  • 3.9K提交
• 题目提供者 HansBug
• 标签 云端↑
• 难度 提高+/省选-
• 时空限制 1s / 128MB

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.将某区间每一个数乘上x

3.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

输出格式：

输出包含若干行整数，即为所有操作3的结果。

输入输出样例

输入样例#1：

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

输出样例#1：

17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

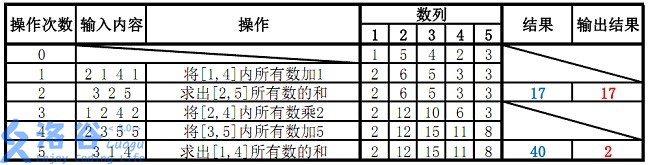
故输出应为17、2（40 mod 38=2）

思路:

　　线段树模板

坑点:

　　1）在更新加的时候要记得看一下爸爸的乘，必须先乘上再进行加

　　2）一定要随时记得%p！！！

上代码=u=:

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#define LL long long
#define lson (l+r)<<1
#define rson (l+r)<<1|1
using namespace std;

const int M = ;
LL n,m,sum,p;
LL ci[M];

struct C {
    LL l,r;
    LL add,multiply;
    LL w;
}t[M*];

LL readin()
{
    LL f=,x=;char ch=getchar();
    while(ch<''||ch>'')
    {if(ch=='-') f=-;ch=getchar();}
    while(ch<=''&&ch>='')
    {x=x*+ch-'',ch=getchar();}
    return (LL)x*f;
}

void builds(LL l,LL r,LL k)
{
    t[k].l=l,t[k].r=r;
    t[k].add=,t[k].multiply=;
    if(l==r)
    {
        t[k].w=ci[l];
        return;
    }
    LL mid=(l+r)>>;
    builds(l,mid,lson),builds(mid+,r,rson);
    t[k].w=(t[lson].w+t[rson].w)%p;
}

void down(LL k)
{
    LL l=t[k].l,r=t[k].r;
    t[lson].add=(t[lson].add*t[k].multiply+t[k].add)%p;
    t[rson].add=(t[rson].add*t[k].multiply+t[k].add)%p;
    t[lson].multiply=(t[lson].multiply*t[k].multiply)%p;
    t[rson].multiply=(t[rson].multiply*t[k].multiply)%p;
    t[lson].w=(t[k].add*(t[lson].r-t[lson].l+)%p+t[lson].w*t[k].multiply%p)%p;
    t[rson].w=(t[k].add*(t[rson].r-t[rson].l+)%p+t[rson].w*t[k].multiply%p)%p;
    t[k].add=,t[k].multiply=;
}

void Multiply(LL a,LL b,LL k,LL cheng)
{
    if(a<=t[k].l && t[k].r<=b)
    {
        t[k].w=t[k].w*cheng%p;
        t[k].add=t[k].add*cheng%p;
        t[k].multiply=t[k].multiply*cheng%p;
        return;
    }
    down(k);
    LL l=t[k].l,r=t[k].r;
    LL mid=(l+r)>>;
    if(a<=mid) Multiply(a,b,lson,cheng);
    if(b>mid)  Multiply(a,b,rson,cheng);
    t[k].w=(t[lson].w+t[rson].w)%p;
}

void Add(LL a,LL b,LL k,LL jia)
{
    if(a<=t[k].l && t[k].r<=b)
    {
        t[k].add=(t[k].add+jia)%p;
        t[k].w=(t[k].w+jia*(t[k].r-t[k].l+))%p;
        return;
    }
    down(k);
    LL l=t[k].l,r=t[k].r;
    LL mid=(l+r)>>;
    if(a<=mid) Add(a,b,lson,jia);
    if(b>mid)  Add(a,b,rson,jia);
    t[k].w=(t[lson].w+t[rson].w)%p;
}

LL Sum(LL a,LL b,LL k)
{
    if(a<=t[k].l && t[k].r<=b)
        return t[k].w%p;
    down(k);
    LL ans=;
    LL l=t[k].l,r=t[k].r;
    LL mid=(l+r)>>;
    if(a<=mid) ans=Sum(a,b,lson)%p;
    if(b>mid) ans+=Sum(a,b,rson)%p;
    return ans%p;
}

int main()
{
    n=readin(),m=readin(),p=readin();
    for(int i=;i<=n;i++)
        ci[i]=readin();
    builds(,n,);
    LL a,b,v;
    for(int i=,q;i<=m;i++)
    {
        scanf("%d",&q);
        switch(q)
        {
            case :
                a=readin(),b=readin(),v=readin();
                Multiply(a,b,,v%p);
                break;
            case :
                a=readin(),b=readin(),v=readin();
                Add(a,b,,v%p);
                break;
            default:
                a=readin(),b=readin();
                sum=Sum(a,b,)%p;
                printf("%lld\n",sum);
        }
    }
    return ;
}