java源码-ReentrantLock源码分析-2

继续上篇ReentrantLock分析如何唤醒线程；

当调用lock.unlock()方法最终调用AQS类中的release方法，开始释放锁

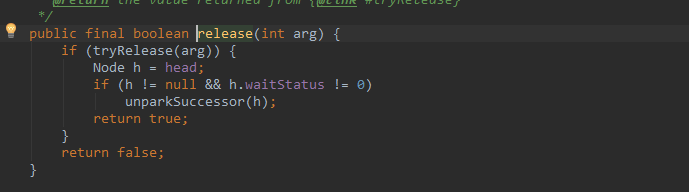
tryRelease(1)方法在Sync对象中实现，首先会检查当前占用锁线程是否是释放线程，如果不是则抛出异常，然后再设置state为0，因为独占锁只有一个线程可以操作，所以不需要cas操作

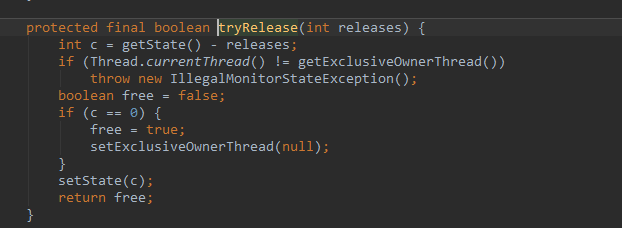
接下来看release(1)方法，获取头节点，判断如果不为0则调用unparkSuccessor(node)方法，首先更新头节点状态为0，获取next节点，

如果next节点为空或者大于0（被取消）则从tail开始找最前面的状态小于0的节点，如果找到唤醒此节点的线程。

然后回到被唤醒线程阻塞的parkAndCheckInterrupt()方法，继续执行返回线程中断状态并清除中断状态

然后如果是调用 lock.lock()方法的话 ,线程如果处于中断状态还会继续获取锁，直到获取锁成功。然后根据中断状态再执行自我中断。

如果是调用lockInterruptibly()/trylock()等方法如果线程被中断，会直接抛出异常，让业务程序自己处理中断请求。

大概ReentrantLock总体源码分析算结束了，如果有不对的地方欢迎指出