张量(tensor)的广播
在使用numpy 对张量(数组)进行操作时,两个形状相同的张量进行加减等运算很容易理解,那么不同形状的张量之间的运算是通过广播来实现的。广播实际上很简单,但是弄清楚是也花了不小功夫,这里记录一下。
广播的目的是将两个不同形状的张量 变成两个形状相同的张量,即先对小的张量添加轴(使其ndim与较大的张量相同),在把较小的张量沿着新轴重复(使其shape与较大的相同)
广播的的限制条件为:两个张量的 trailing dimension(从后往前算起的维度)的轴长相等 或 其中一个的长度为1
import numpy as np
a=np.arange(0,12)
a=a.reshape(3,4)
b=np.arange(0,4)
print(a)
#[[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]] print(b)
#[0 1 2 3] print(a.shape)
#(3, 4) print(b.shape)
#(4,) print(a.ndim)
#
print(b.ndim)
# a+b #array([[ 0, 2, 4, 6],
# [ 4, 6, 8, 10],
# [ 8, 10, 12, 14]])
上述 a+b 的计算过程等价为:
(1)先将b添加一个轴 即
(2)在将b沿着 新加的轴进行重复
b.reshape(1,4)
#array([[0, 1, 2, 3]]) c=np.array([b,b,b])
#array([[0, 1, 2, 3],
# [0, 1, 2, 3],
# [0, 1, 2, 3]]) a+c #array([[ 0, 2, 4, 6],
# [ 4, 6, 8, 10],
# [ 8, 10, 12, 14]])
其他几个例子
x=np.arange(0,12)
x=x.reshape(3,4,1)
x
y=np.arange(0,8)
y=y.reshape(4,2)
y
q=x+y
q.shape
#(3,4,2)
x=np.arange(0,12)
x=x.reshape(3,4,1)
x
z=np.arange(0,2)
z=z.reshape(1,2)
z
q=x+z
q.shape
#(3,4,2)
x :  y
y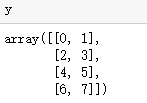 z
z 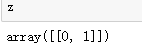 x+y
x+y  x+z
x+z 
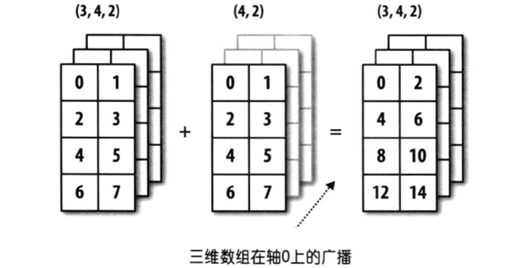
最后放上几个图片便于理解

张量(tensor)的广播的更多相关文章
- tensorflow中张量(tensor)的属性——维数(阶)、形状和数据类型
tensorflow的命名来源于本身的运行原理,tensor(张量)意味着N维数组,flow(流)意味着基于数据流图的计算,所以tensorflow字面理解为张量从流图的一端流动到另一端的计算过程. ...
- 张量 (tensor) 是什么?
对于大部分已经熟练的数学和物理工作者, 这实在是一个极为基础的问题. 但这个问题在我刚接触张量时也困扰了我很久. 张量的那么多定义, 究竟哪些是对的? (显然都是对的. ) 它们的关系是什么? 我尽可 ...
- 如何理解张量tensor
1 关于张量的四种定义 “张量”在不同的运用场景下有不同的定义. 第一个定义,张量是多维数组,这个定义常见于各种人工智能软件.听起来还好理解.--本文仅解释此种 2 多维数组 从第一个定义:张量是多维 ...
- 2、介绍在TensorFlow当中使用不同的方式创建张量tensor
import tensorflow as tf from tensorflow.python.framework import ops ops.reset_default_graph() #开始一个计 ...
- AI - TensorFlow - 张量(Tensor)
张量(Tensor) 在Tensorflow中,变量统一称作张量(Tensor). 张量(Tensor)是任意维度的数组. 0阶张量:纯量或标量 (scalar), 也就是一个数值,例如,\'Howd ...
- pytorch中tensor张量数据基础入门
pytorch张量数据类型入门1.对于pytorch的深度学习框架,其基本的数据类型属于张量数据类型,即Tensor数据类型,对于python里面的int,float,int array,flaot ...
- 学习笔记DL004:标量、向量、矩阵、张量,矩阵、向量相乘,单位矩阵、逆矩阵
线性代数,面向连续数学,非离散数学.<The Matrix Cookbook>,Petersen and Pedersen,2006.Shilov(1977). 标量.向量.矩阵.张量. ...
- 深度学习框架PyTorch一书的学习-第三章-Tensor和autograd-1-Tensor
参考https://github.com/chenyuntc/pytorch-book/tree/v1.0 希望大家直接到上面的网址去查看代码,下面是本人的笔记 Tensor Tensor可以是一个数 ...
- 【tensorflow2.0】张量的结构操作
张量的操作主要包括张量的结构操作和张量的数学运算. 张量结构操作诸如:张量创建,索引切片,维度变换,合并分割. 张量数学运算主要有:标量运算,向量运算,矩阵运算.另外我们会介绍张量运算的广播机制. 本 ...
- Tensorflow学习笔记2:About Session, Graph, Operation and Tensor
简介 上一篇笔记:Tensorflow学习笔记1:Get Started 我们谈到Tensorflow是基于图(Graph)的计算系统.而图的节点则是由操作(Operation)来构成的,而图的各个节 ...
随机推荐
- Tekla 导出ifc并浏览
Tekla导出IFC
- Spring cloud微服务安全实战-4-8Zuul网关安全开发(一)
安全相关的代码和业务逻辑相关的代码实际上是在一个应用里面的,在这个应用里面,我们需要去,这个应用本身的处理逻辑里面需要去处理令牌和用户信息之间的转换. 然后我们需要去知道认证服务器的地址,这些都是耦合 ...
- 背诵四种清净明诲断淫(愿众生断淫得究竟解脱) (转自学佛网:http://www.xuefo.net/nr/article50/495158.html)
一.为什么要戒邪淫.断淫欲 <寿康宝鉴>:盖淫念一生,诸念皆起.邪缘未凑生妄心;勾引无计,生机械心;少有阻碍,生嗔恨心;欲情颠倒,生贪着心;羡人有之,生嫉妒心;夺人之爱,生杀害心.廉耻丧尽 ...
- java 连接 mongodb 及使用
MongoDB是当今非常流行的一款NoSQL数据库,本文介绍如何使用MongoDB的Java驱动来操作MongoDB. 一.引入MongoDB Java Driver包 如果需要操作MongoDB的J ...
- Python - Django - 模板语言之 Tags(标签)
标签使用 {% %} 注释语句:{# #} for 循环: views.py: from django.shortcuts import render, redirect, HttpResponse ...
- Cas(06)——基于数据库的认证
基于数据库的认证 目录 1.1 BindModeSearchDatabaseAuthenticationHandler 1.2 QueryDatabaseAuthenticatio ...
- 服务发现--初识Consul
前言 服务注册.服务发现作为构建微服务架构得基础设施环节,重要性不言而喻.在当下,比较热门用于做服务注册和发现的开源项目包括zookeeper.etcd.euerka和consul.今天在这里对近期学 ...
- CF1237D Balanced Playlist
思路:假设从第i首歌开始听,结束位置为j,那么从第i+1首歌开始听,结束位置一定不早于j.可以用反证法证明.想到这一点,就不难解决了. 实现: #include <bits/stdc++.h&g ...
- C++ 宏和模板简介
参考<21天学通C++>第14章节,对C++中的宏和模板进行了学习,总结起来其主要内容如下: (1) 预处理器简介 (2) 关键字#define与宏 (3) 模板简介 (4) 如何编写函数 ...
- C#本地修改器
C#本地修改器 C# 制作外挂常用的API C#做外挂的常用API,本人用了很久,基本没发现问题 using System; using System.Collections.Generic; usi ...
