阶段5 3.微服务项目【学成在线】_day02 CMS前端开发_11-webpack研究-npm和cnpm安装配置

node.js安装完成后,就自动安装了webpack。
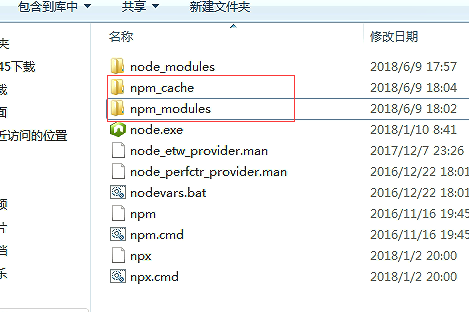
npm -v:查看npm安装的版本


当前安装目录默认的包

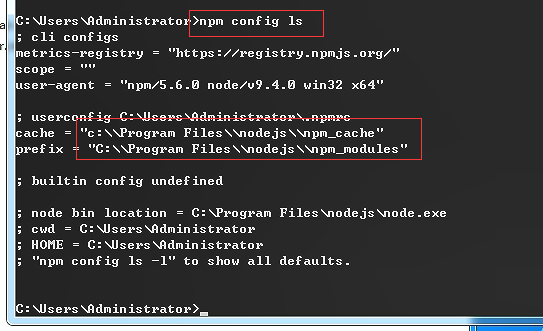
在node.js的目录下创建两个文件夹


这样路径就被修改成功了
cnpm
npm install -g cnpm --registry=https://registry.npm.taobao.org
cnpm -v:正确安装

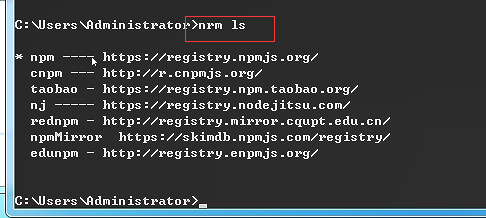
改成taobao镜像


总结

阶段5 3.微服务项目【学成在线】_day02 CMS前端开发_11-webpack研究-npm和cnpm安装配置的更多相关文章
- 微服务项目开发学成在线_day02 CMS前端开发
1 Vue.js与Webpack研究 开发版的浏览器:https://www.google.cn/intl/zh-CN/chrome/dev/ 前端的开发框架:微服务项目开发学成在线_Vue.js与W ...
- 阶段5 3.微服务项目【学成在线】_day04 页面静态化_16-页面静态化-模板管理-模板制作
这是轮播图的原始文件 运行门户需要把 nginx启动起来 单独运行轮播图.把里面的css的引用都加上网址的url 这就是单独访问到的轮播图的效果 轮播图模板的地址: 阶段5 3.微服务项目[学成在线] ...
- 阶段5 3.微服务项目【学成在线】_day02 CMS前端开发_16-CMS前端工程创建-导入系统管理前端工程
提供了基于脚手架封装好的前端工程 H:\BaiDu\黑马传智JavaEE57期 2019最新基础+就业+在职加薪\阶段5 3.微服务项目[学成在线]·\day02 CMS前端开发\资料\xc-ui-p ...
- 阶段5 3.微服务项目【学成在线】_day16 Spring Security Oauth2_03-用户认证技术方案-Oauth2协议
2.2 Oauth2认证 2.2.1 Oauth2认证流程 第三方认证技术方案最主要是解决认证协议的通用标准 问题,因为要实现 跨系统认证,各系统之间要遵循一定的 接口协议. OAUTH协议为用户资源 ...
- 阶段5 3.微服务项目【学成在线】_day16 Spring Security Oauth2_01-用户认证需求分析
1.1 用户认证与授权 截至目前,项目已经完成了在线学习功能,用户通过在线学习页面点播视频进行学习.如何去记录学生的学习过程 呢?要想掌握学生的学习情况就需要知道用户的身份信息,记录哪个用户在什么时间 ...
- 阶段5 3.微服务项目【学成在线】_day09 课程预览 Eureka Feign_05-Feign远程调用-客户端负载均衡介绍
2 Feign远程调用 在前后端分离架构中,服务层被拆分成了很多的微服务,服务与服务之间难免发生交互,比如:课程发布需要调用 CMS服务生成课程静态化页面,本节研究微服务远程调用所使用的技术. 下图是 ...
- 阶段5 3.微服务项目【学成在线】_day09 课程预览 Eureka Feign_02-Eureka注册中心-搭建Eureka单机环境
我们先搭建单机环境 govern是治理的意思, 这样就把工程创建好了 创建包 创建SpringBoot的启动类. 在父工程里面已经确定了Spring Cloud的版本了.相当于锁定了版本 接下里只需要 ...
- 阶段5 3.微服务项目【学成在线】_day09 课程预览 Eureka Feign_04-Eureka注册中心-将服务注册到Eureka Server
cms相当于客户端 配置客户端的信息 后面加逗号分隔开 50102表示向两台eureka服务上报服务,如果有一台死掉了 那么还可以上另外的一台去注册服务 直接把ip注册到eureka 启动类加注解 重 ...
- 阶段5 3.微服务项目【学成在线】_day09 课程预览 Eureka Feign_01-Eureka注册中心-Eureka介绍
1 Eureka注册中心 1.1 需求分析 在前后端分离架构中,服务层被拆分成了很多的微服务,微服务的信息如何管理?Spring Cloud中提供服务注册中 心来管理微服务信息. 为什么 要用注册中心 ...
随机推荐
- [daily]使用iptables配置NAT的命令速查
时常,快速的配置一个临时的NAT环境是很常用需求. 但是,每次我都要读iptables的手册,才能配出来.所以,备忘一个速查. DNAT: iptables -t nat -A PREROUTING ...
- Django:总结setting中的配置
一.Django setting配置说明 二.setting配置一览 一.Django setting配置说明 1.基础 DJANGO_SETTING_MODULE环境变量:让settings模块被包 ...
- 10_Azkaban案例实践3_Command操作HDFS
HDFS操作任务 1.创建job描述文件 # fs.job type=command command=/usr/local/src/hadoop-2.6.4/bin/hadoop fs -mkdir ...
- Mha-Atlas-MySQL高可用方案实践
一,mysql-mha环境准备 1.1 实验环境: 1.1 实验环境: 主机名 IP地址(NAT) 描述 mysql-master eth0:10.1.1.154 系统:CentOS6.5(6.x都可 ...
- Android.mk走读与Cmake配置
Android.mk认识: 在上一次[https://www.cnblogs.com/webor2006/p/9946061.html]中学会了用NDK提供的交叉编译工程编译成Android能运行的可 ...
- Python命令行创建虚拟环境
Python命令行创建虚拟环境 安装virtualenv 启动命令行,执行命令pip install -U virtualenv 创建一个新的虚拟环境 执行命令python -m virtualenv ...
- django考点
django考点 1 列举Http请求中常见的请求方式2 谈谈你对HTTP协议的认识.1.1 长连接3 简述MVC模式和MVT模式4 简述Django请求生命周期5 简述什么是FBV和CBV6 谈一谈 ...
- Linux系统进程的知识总结,进程与线程之间的纠葛...
来源:嵌入式ARM 当一个程序开始执行后,在开始执行到执行完毕退出这段时间内,它在内存中的部分就叫称作一个进程. Linux 是一个多任务的操作系统,也就是说,在同一时间内,可以有多个进程同时执行.我 ...
- MySQL常见水平分表技术方案
根据经验,Mysql表数据一般达到百万级别,查询效率会很低,容易造成表锁,甚至堆积很多连接,直接挂掉:水平分表能够很大程度较少这些压力. 1.按时间分表 这种分表方式有一定的局限性,当数据有较强的实效 ...
- nginx+uwsgi+bottle python服务器部署
一.安装nginx(如果服务器上已经有nginx了,则无需重复安装) sudo apt-get install nginx 二.nginx配置,例如:/etc/nginx/conf.d/digger. ...
