[BZOJ1576]安全路经Travel
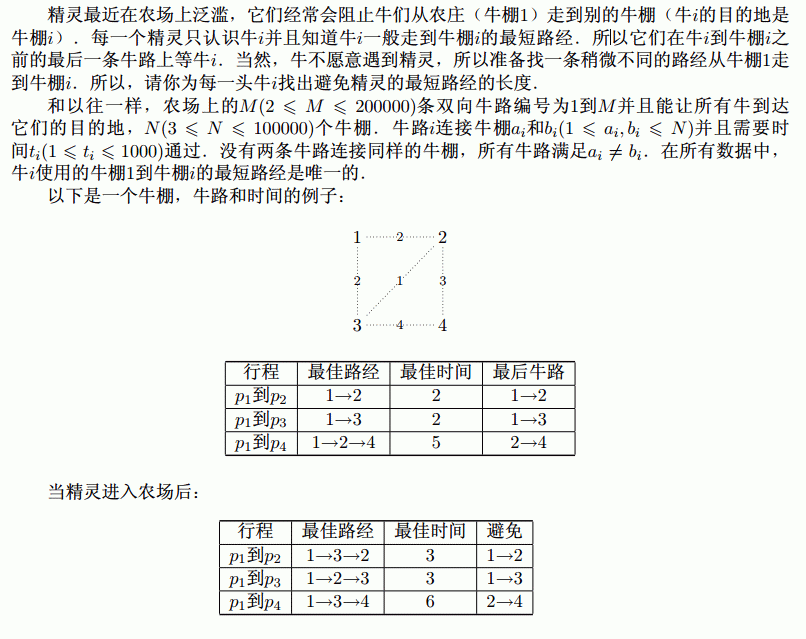
题目大意:从1号点出发,到每个点的最短路的最后一条边不能被访问,求此时1号点到其他点的最短路
建立最短路树,对于一条非树边,把它加进去会形成一个环和一条链,如图:
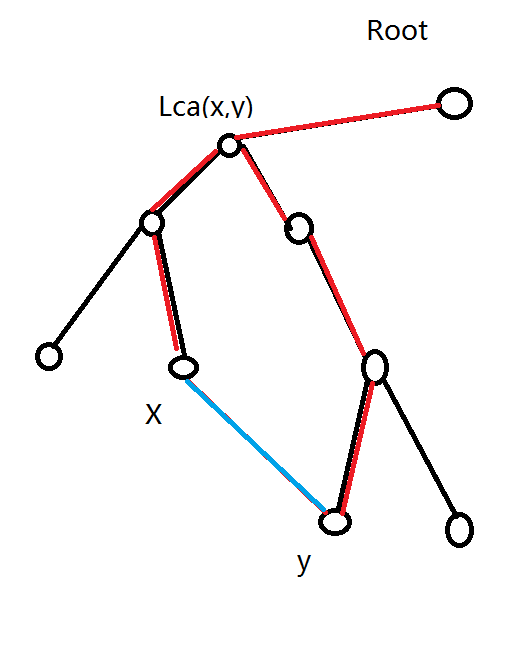
即红色和蓝色路径构成的图,它的长度为$len=dis[x]+dis[y]+w[x][y]$,对于这个环上的任意一点$i$,我们都可以用$len-dis[i]$来更新答案。
如果我们把$len$按从小到大排序,显然每对$(x,y)$只会更新环内没被更新的点,这时我们可以用并查集加速维护
因为每个点只会被更新一次,所以更新完后这个点就没有再被访问的必要,直接把这个点的父亲指向这个环的$LCA$即可(因为环内的点已经全部被更新完了)
[BZOJ1576]安全路经Travel的更多相关文章
- 【BZOJ1576】[Usaco2009 Jan]安全路经Travel 最短路+并查集
[BZOJ1576][Usaco2009 Jan]安全路经Travel Description Input * 第一行: 两个空格分开的数, N和M * 第2..M+1行: 三个空格分开的数a_i, ...
- 【思维题 并查集 图论】bzoj1576: [Usaco2009 Jan]安全路经Travel
有趣的思考题 Description Input * 第一行: 两个空格分开的数, N和M * 第2..M+1行: 三个空格分开的数a_i, b_i,和t_i Output * 第1..N-1行: 第 ...
- bzoj 1576: [Usaco2009 Jan]安全路经Travel 树链剖分
1576: [Usaco2009 Jan]安全路经Travel Time Limit: 10 Sec Memory Limit: 64 MB Submit: 665 Solved: 227[Sub ...
- BZOJ1576: [Usaco2009 Jan]安全路经Travel(树链剖分)
Description Input * 第一行: 两个空格分开的数, N和M * 第2..M+1行: 三个空格分开的数a_i, b_i,和t_i Output * 第1..N-1行: 第i行包含一个数 ...
- BZOJ1576 [Usaco2009 Jan]安全路经Travel
首先用Dijkstra做出最短路生成树,设dis[p]为1到p点的最短路长度 对于一条不在生成树上的边u -> v,不妨设fa为u.v的lca 则一fa到v的路径上的任意点x都可以由u达到,走的 ...
- [Usaco2009 Jan]安全路经Travel BZOJ1576 Dijkstra+树链剖分+线段树
分析: Dijkstra求最短路树,在最短路树上进行操作,详情可见上一篇博客:http://www.cnblogs.com/Winniechen/p/9042937.html 我觉得这个东西不压行写出 ...
- BZOJ1576: [Usaco2009 Jan]安全路经Travel(最短路 并查集)
题意 给你一张无向图,保证从1号点到每个点的最短路唯一.对于每个点求出删掉号点到它的最短路上的最后一条边(就是这条路径上与他自己相连的那条边)后1号点到它的最短路的长度 Sol emmm,考场上想了个 ...
- [BZOJ1576] [Usaco2009 Jan]安全路经Travel(堆优化dijk + (并查集 || 树剖))
传送门 蒟蒻我原本还想着跑两边spfa,发现不行,就gg了. 首先这道题卡spfa,所以需要用堆优化的dijkstra求出最短路径 因为题目中说了,保证最短路径有且只有一条,所以可以通过dfs求出最短 ...
- bzoj 1576 [Usaco2009 Jan]安全路经Travel(树链剖分,线段树)
[题意] 给定一个无向图,找到1-i所有的次短路经,要求与最短路径的最后一条边不重叠. [思路] 首先用dijkstra算法构造以1为根的最短路树. 将一条无向边看作两条有向边,考察一条不在最短路树上 ...
随机推荐
- 【转】SignalR来做实时Web聊天
本章和大家分享的内容是使用Signal R框架创建个简易的群聊功能,主要讲解如何在.Net的MVC中使用这个框架,由于这个项目有官方文档(当然全英文),后面也不打算写分享篇了,主要目的是让朋友们在需要 ...
- [转载]Elasticsearch、MongoDB和Hadoop比较
IT界在过去几年中出现了一个有趣的现象.很多新的技术出现并立即拥抱了“大数据”.稍微老一点的技术也会将大数据添进自己的特性,避免落大部队太远,我们看到了不同技术之间的边际的模糊化.假如你有诸如Elas ...
- kafka Detailed Replication Design V3
参考,https://cwiki.apache.org/confluence/display/KAFKA/kafka+Detailed+Replication+Design+V3 Major chan ...
- 基于spring的quartz定时框架,实现简单的定时任务功能
在项目中,经常会用到定时任务,这就需要使用quartz框架去进行操作. 今天就把我最近做的个人主页项目里面的定时刷新功能分享一下,很简单. 首先需要配置一个配置文件,因为我是基于spring框架的,所 ...
- 软中断和tasklet介绍
今天看了下tasklet,重点分析了其和软中断的关系,特此记录 关于软中断,在之前的中断文章中已经有所介绍,这里就不多说了,只是说明下,系统中默认支持32种软中断,而实际上系统定义的软中断仅有以下几种 ...
- Python并行编程(八):with语法
1.基本概念 当有两个相关的操作需要在一部分代码块前后分别执行的时候,可以使用with语法自动完成.同时,使用with语法可以在特定的地方分配和释放资源,因此,with语法也叫作"上下文管理 ...
- des/3des
一.python 1. des3 python平台的DES3 + base64 加密解密, 有两个常用的库pycrypto和pyDes 1)pycrypto des3.py #coding=utf-8 ...
- PAT 1051 Pop Sequence[栈][难]
1051 Pop Sequence (25 分) Given a stack which can keep M numbers at most. Push N numbers in the order ...
- 一、html
一.html相关概念 html是 htyper text markup language 即超文本标记语言,超文本就是指页面内可以包含图片.链接,甚至音乐.程序等非文字元素,而标记语言:即标记(标签) ...
- Activity 间 bundle 传递参数
activity_main.xml <TableLayout xmlns:android="http://schemas.android.com/apk/res/android&quo ...
