[APIO / CTSC2007]数据备份 --- 贪心

[APIO / CTSC 2007]数据备份

题目描述

你在一家 IT 公司为大型写字楼或办公楼(offices)的计算机数据做备份。

然而数据备份的工作是枯燥乏味的，因此你想设计一个系统让不同的办公楼彼此之间互相备份，而你则坐在家中尽享计算机游戏的乐趣。

已知办公楼都位于同一条街上。你决定给这些办公楼配对(两个一组)。

每一对办公楼可以通过在这两个建筑物之间铺设网络电缆使得它们可以互相备份。

然而，网络电缆的费用很高。当地电信公司仅能为你提供 K 条网络电缆，这意味着你仅能为 K 对办公楼(或总计 2K 个办公楼)安排备份。

任一个办公楼都属于唯一的配对组(换句话说，这 2K 个办公楼一定是相异的)。

此外，电信公司需按网络电缆的长度(公里数)收费。

因而，你需要选择这 K对办公楼使得电缆的总长度尽可能短。

换句话说，你需要选择这 K 对办公楼，使得每一对办公楼之间的距离之和(总距离)尽可能小。

下面给出一个示例，假定你有 5 个客户，其办公楼都在一条街上，如下图所示。

这 5 个办公楼分别位于距离大街起点 1km, 3km, 4km, 6km 和 12km 处。电信公司仅为你提供 K=2 条电缆。

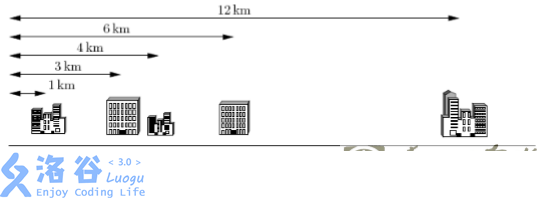
上例中最好的配对方案是将第 1 个和第 2 个办公楼相连，第 3 个和第 4 个办公楼相连。

这样可按要求使用 K=2 条电缆。第 1 条电缆的长度是 3km―1km = 2km，第 2 条电缆的长度是 6km―4km = 2 km。

这种配对方案需要总长 4km 的网络电缆，满足距离之和最小的要求。

输入格式：

输入文件的第一行包含整数 n 和 k，其中 n(1≤n≤100 000)表示办公楼的数目，k(1≤k≤n/2)表示可利用的网络电缆的数目。

接下来的 n 行每行仅包含一个整数(0≤s≤1000 000 000), 表示每个办公楼到大街起点处的距离。这些整数将按照从小到大的顺序依次出现。

输出格式：

输出文件应当由一个正整数组成，给出将 2K 个相异的办公楼连成 K 对所需的网络电缆的最小总长度。

两个贪心混成的题。

第一个贪心：所选的网络电缆一定是连接相邻的办公楼。

证明：（虽然感觉像就非常像）如果有两对点不满足，那么一定是下列情况中的一种：

A1  A2  A3  A4  A5

1.A1连A2，A3连A5，很明显，A3连A4更优

2.A1连A3，A4连A2，那么A1连A2，A3连A4也更优（也说明连的区间不重合）

这样，可以知道相当于是在\((n-1)\)线段中选取\(k\)条不共点的线段。

也就是说，不能选择相邻的线段。

第二个贪心：同种树

考虑选了线段\(i\)，怎么样表示选了线段\(i+1\)和线段\(i-1\)后比线段\(i\)更优呢？

选择线段\(i\)后，将线段\(i+1\)和线段\(i-1\)标记为不可选。

往堆中新添一个点\(p\)，权值为\(val[i+1]+val[i-1]-val[i]\)，那么选了点\(p\)就表示选择了线段\(i+1\)以及线段\(i-1\)

容易扩展到多个点的情况。

此时，单独的记录\(i+1\)和\(i-1\)是不行的，而是需要用一个链表来记录左右的节点。

时间复杂度\(O(k* \log n)\)

代码在此