[吴恩达机器学习笔记]12支持向量机3SVM大间距分类的数学解释

12.支持向量机

觉得有用的话,欢迎一起讨论相互学习~Follow Me

参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广

12.3 大间距分类背后的数学原理- Mathematics Behind Large Margin classification

向量内积

1. 假设有两个向量\(u=\begin{bmatrix}u_1\\u_2\\ \end{bmatrix}\),向量\(v=\begin{bmatrix}v_1\\v_2\\ \end{bmatrix}\)，其中向量的内积表示为\(u^Tv\).假设\(u_1\)表示为u在坐标轴横轴上的投影，而\(u_2\)表示为u在坐标轴纵轴上的投影，则向量u的欧几里得长度可表示为\(\parallel u \parallel\) , 且有\(\parallel u \parallel=\sqrt{u_1^{2}+u_2^{2}}\)
   

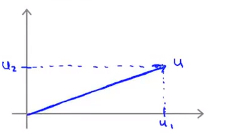
2. 对于向量的内积\(u^{T}v\) ,可以视为 v向量在u向量上的投影p乘以u向量的长度，这两者都为实数，且当v向量的投影与u向量同方向时，p取正号，否则p取负号 即有式子 \[u^{T}v=P * \parallel u \parallel=u_1v_1+u_2v_2\]
   

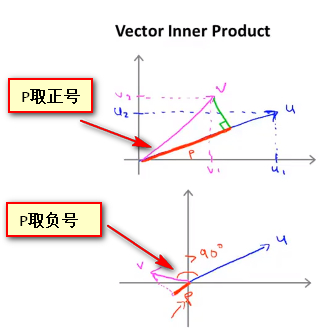
   向量内积研究SVM目标函数

   

• 为了更容易分析问题只保留了损失函数的后半部分而去掉了C及其乘积项。 ，原始损失函数如下图：
  
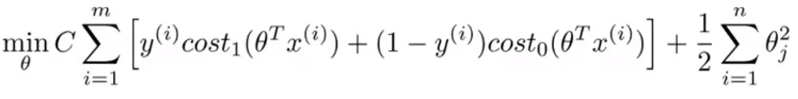
• 为简化起见，忽略掉截距，设置损失函数中参数\(\theta_0\)为0，设置特征数n=2. ，则简化后的式子可写为:
  

• 因此可以认为SVM的目的就是最小化向量\(\theta\) 范数的平方或者说是长度的平方

  \(\theta^{T}x\)的意义

• 给定参数向量 θ 给定一个样本x， 计算其二者的乘积，这其中的含义是什么？ 对于\(\theta^{T}x\)其相当于向量内积\(u^{T}v\)
  
  

1. 首先，对于训练样本\(x^{(i)}\),其在x轴上的取值为\(x^{(i)}_{1}\),其在y轴上的取值为\(x^{(i)}_{2}\) ,此时 将其视为始于原点，终点位于训练样本的向量
2. 然后将参数 \(\theta\) 也视为向量且其在横轴上的投影为 \(\theta_1\) ,其在纵轴上的投影为 \(\theta_2\)
3. 使用之前的方法，将训练样本投影到参数向量 θ，使用 \(p_{(i)}\)来表示第 i 个训练样本在参数向量\(\theta\)上的投影。 即有 \[\theta^{T}x^{(i)}=p_{(i)}\parallel \theta\ \parallel=\theta_1x_1^{(i)}+\theta_2x_2^{(i)}\]
   

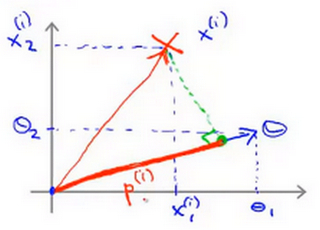
4. \(x_{(i)}\)代表从原点出发连接到第i个样本点的向量，是可正可负的，分别表示正样本和负样本；\(p^{(i)}\)表示样本向量\(x_{(i)}\)到参数向量\(\theta\)上的投影，其也是可正可负的，同方向为正负方向为负 ，对于SVM中\(\theta^{T}x^{(i)}\ge1或者\theta^{T}x^{(i)}\le-1\)的约束也可以被 \(p^{(i)}x\ge1\)这个约束所代替

   从\(\theta^{T}x\)到大间距

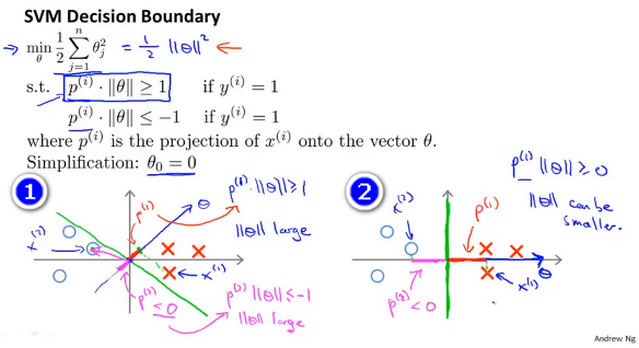
• 首先为方便起见设置 \(\theta_0=0\) ,且只选取两个特征，即\(\theta_1 和 \theta_2\) ,则参数\(\theta\) 可以表示成一条过原点的直线，且 决策界 与\(\theta\)直线垂直。
• 反证法 如下图所示(1)，y轴右边的表示正样本，而y轴左边的表示负样本，蓝线表示参数\(\theta\)，绿线表示决策界 ，很明显这条决策界很不好，因为其与正负样本的间距太小了。 通过将样本投影到\(\theta\)上可以得到p,此时正负样本的||p||都很小，根据SVM的公式||p|| * ||\(\theta\)||>=1,则其必须使||\(\theta\)||很大才能满足条件，这和目标函数希望找到一个小的参数\(\theta\)的目的是矛盾的，这表明这并不是一条好的决策界
• 而图(2)中x在\(\theta\)的投影p就相对的大一些，这样在满足公式\(||p|| * ||\theta||>=1\)需要的||\(\theta\)||就会小一些，这和SVM的优化目标是一致的。所以 好的SVM的优化结果中，决策界的间距一定比较大