Codeforces Round #409 (rated, Div. 2, based on VK Cup 2017 Round 2) D. Volatile Kite

地址：http://codeforces.com/contest/801/problem/D

题目：

D. Volatile Kite

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a convex polygon P with n distinct vertices p1, p2, ..., pn. Vertex pi has coordinates (xi, yi) in the 2D plane. These vertices are listed in clockwise order.

You can choose a real number D and move each vertex of the polygon a distance of at most D from their original positions.

Find the maximum value of D such that no matter how you move the vertices, the polygon does not intersect itself and stays convex.

Input

The first line has one integer n (4 ≤ n ≤ 1 000) — the number of vertices.

The next n lines contain the coordinates of the vertices. Line i contains two integers xi and yi ( - 109 ≤ xi, yi ≤ 109) — the coordinates of the i-th vertex. These points are guaranteed to be given in clockwise order, and will form a strictly convex polygon (in particular, no three consecutive points lie on the same straight line).

Output

Print one real number D, which is the maximum real number such that no matter how you move the vertices, the polygon stays convex.

Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely, let's assume that your answer is a and the answer of the jury is b. The checker program will consider your answer correct if .

Examples

input

4
0 0
0 1
1 1
1 0

output

0.3535533906

input

6
5 0
10 0
12 -4
10 -8
5 -8
3 -4

output

1.0000000000

Note

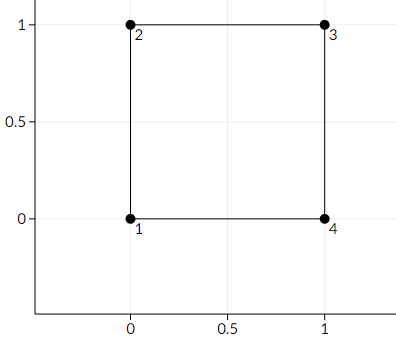
Here is a picture of the first sample

Here is an example of making the polygon non-convex.

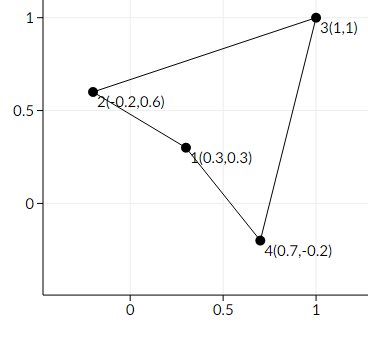
This is not an optimal solution, since the maximum distance we moved one point is  ≈ 0.4242640687, whereas we can make it non-convex by only moving each point a distance of at most  ≈ 0.3535533906.

思路：这题看起来很复杂，但是看下样例一的图后会发现一个结论：

　　在相邻的三个点a,b,c中，能移动的最大距离d就是b到直线ac的距离的一半。

　　证明：当d大于一半时，凸包会被破坏。

　　　　　当d小于一半时，凸包仍然存在（即可以继续移动）

　　

　　所以贴个求点到直线的模板，然后扫一遍所有点，求出所有可移动距离的最大值中的最小值即可。

　　（完整代码模板我博客有

 #include <bits/stdc++.h>

 using namespace std;

 #define MP make_pair
 #define PB push_back
 typedef long long LL;
 typedef pair<int,int> PII;
 const double eps=1e-;
 const double pi=acos(-1.0);
 const int K=1e6+;
 const int mod=1e9+;

 //点
 class Point
 {
 public:
     double x, y;

     Point(){}
     Point(double x, double y):x(x),y(y){}

     bool operator < (const Point &_se) const
     {
         return x<_se.x || (x==_se.x && y<_se.y);
     }
     /*******判断ta与tb的大小关系*******/
     static int sgn(double ta,double tb)
     {
         if(fabs(ta-tb)<eps)return ;
         if(ta<tb)   return -;
         return ;
     }
     static double xmult(const Point &po, const Point &ps, const Point &pe)
     {
         return (ps.x - po.x) * (pe.y - po.y) - (pe.x - po.x) * (ps.y - po.y);
     }
     friend Point operator + (const Point &_st,const Point &_se)
     {
         return Point(_st.x + _se.x, _st.y + _se.y);
     }
     friend Point operator - (const Point &_st,const Point &_se)
     {
         return Point(_st.x - _se.x, _st.y - _se.y);
     }
     //点位置相同(double类型)
     bool operator == (const Point &_off) const
     {
         return  Point::sgn(x, _off.x) ==  && Point::sgn(y, _off.y) == ;
     }
     //点位置不同(double类型)
     bool operator != (const Point &_Off) const
     {
         return ((*this) == _Off) == false;
     }
     //两点间距离的平方
     static double dis2(const Point &_st,const Point &_se)
     {
         return (_st.x - _se.x) * (_st.x - _se.x) + (_st.y - _se.y) * (_st.y - _se.y);
     }
     //两点间距离
     static double dis(const Point &_st, const Point &_se)
     {
         return sqrt((_st.x - _se.x) * (_st.x - _se.x) + (_st.y - _se.y) * (_st.y - _se.y));
     }
 };
 //两点表示的向量
 class Line
 {
 public:
     Point s, e;//两点表示，起点[s]，终点[e]
     double a, b, c;//一般式,ax+by+c=0

     Line(){}
     Line(const Point &s, const Point &e):s(s),e(e){}
     Line(double _a,double _b,double _c):a(_a),b(_b),c(_c){}

     //向量与点的叉乘,参数：点[_Off]
     //[点相对向量位置判断]
     double operator /(const Point &_Off) const
     {
         return (_Off.y - s.y) * (e.x - s.x) - (_Off.x - s.x) * (e.y - s.y);
     }
     //向量与向量的叉乘,参数：向量[_Off]
     friend double operator /(const Line &_st,const Line &_se)
     {
         return (_st.e.x - _st.s.x) * (_se.e.y - _se.s.y) - (_st.e.y - _st.s.y) * (_se.e.x - _se.s.x);
     }
     friend double operator *(const Line &_st,const Line &_se)
     {
         return (_st.e.x - _st.s.x) * (_se.e.x - _se.s.x) - (_st.e.y - _st.s.y) * (_se.e.y - _se.s.y);
     }
     //从两点表示转换为一般表示
     //a=y2-y1,b=x1-x2,c=x2*y1-x1*y2
     bool pton()
     {
         a = e.y - s.y;
         b = s.x - e.x;
         c = e.x * s.y - e.y * s.x;
         return true;
     }

     //-----------点和直线（向量）-----------
     //点在向量左边（右边的小于号改成大于号即可,在对应直线上则加上=号）
     //参数：点[_Off],向量[_Ori]
     friend bool operator<(const Point &_Off, const Line &_Ori)
     {
         return (_Ori.e.y - _Ori.s.y) * (_Off.x - _Ori.s.x)
             < (_Off.y - _Ori.s.y) * (_Ori.e.x - _Ori.s.x);
     }

     //点在直线上,参数：点[_Off]
     bool lhas(const Point &_Off) const
     {
         return Point::sgn((*this) / _Off, ) == ;
     }
     //点在线段上,参数：点[_Off]
     bool shas(const Point &_Off) const
     {
         return lhas(_Off)
             && Point::sgn(_Off.x - min(s.x, e.x), ) >  && Point::sgn(_Off.x - max(s.x, e.x), ) <
             && Point::sgn(_Off.y - min(s.y, e.y), ) >  && Point::sgn(_Off.y - max(s.y, e.y), ) < ;
     }

     //点到直线/线段的距离
     //参数： 点[_Off], 是否是线段[isSegment](默认为直线)
     double dis(const Point &_Off, bool isSegment = false)
     {
         ///化为一般式
         pton();

         //到直线垂足的距离
         double td = (a * _Off.x + b * _Off.y + c) / sqrt(a * a + b * b);

         //如果是线段判断垂足
         if(isSegment)
         {
             double xp = (b * b * _Off.x - a * b * _Off.y - a * c) / ( a * a + b * b);
             double yp = (-a * b * _Off.x + a * a * _Off.y - b * c) / (a * a + b * b);
             double xb = max(s.x, e.x);
             double yb = max(s.y, e.y);
             double xs = s.x + e.x - xb;
             double ys = s.y + e.y - yb;
             if(xp > xb + eps || xp < xs - eps || yp > yb + eps || yp < ys - eps)
                 td = min(Point::dis(_Off,s), Point::dis(_Off,e));
         }

         return fabs(td);
     }
 };

 int n;
 Point pt[K];
 Line ta;
 double ans=1e10;
 int main(void)
 {
     cin>>n;
     for(int i=;i<=n;i++)
         scanf("%lf%lf",&pt[i].x,&pt[i].y);
     for(int i=;i<=;i++)
         pt[i+n]=pt[i];
     for(int i=;i<=n;i++)
     {
         ta.s=pt[i],ta.e=pt[i+];
         ans=min(ans,ta.dis(pt[i+])/2.0);
     }
     printf("%.8f\n",ans);
     return ;
 }