在写了第一个app之后，打算上架到各个渠道看看，无意间看到了360的app加固工具

http://jiagu.360.cn/

自己体验了一把，加固过程很傻瓜化，

加固好了之后，还要对app进行二次签名，

最终app体积略微增加了160KB

我们知道app的逆向编译，主要是针对dex进行操作，

查看了加固后的结果，发现dex体积减小了，然后多了Lib目录；猜测这就是360加固保护的成果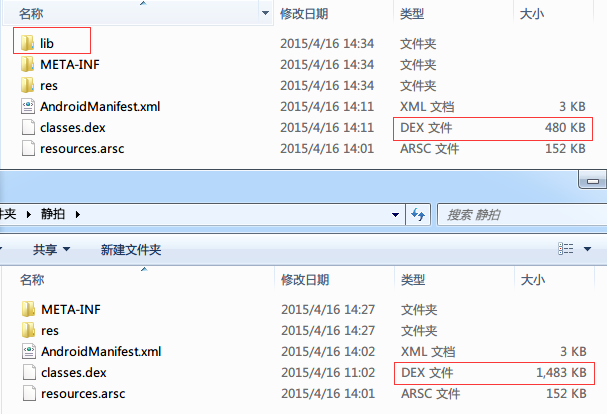

感觉还不错，打算以后发布前都先这么加密下，反正免费的，哈哈

使用360对app安全进行加固的更多相关文章

  1. iOS - app 进行安全加固

    研究了大半年逆向工程了,没在博客做记录,最近看到篇,跟自己的想法不谋而合,摘要下: 运行在越狱设备上的 iOS app,非常容易遭到破解分析,这里我列举一些可以加大破解难度的方法,希望有所帮助. 一些 ...

  2. iOS App的加固保护原理

    本文由  网易云发布. 本文从攻防原理层面解析了iOS APP的安全策略.iOS以高安全性著称,但它并非金刚不坏之身.对于信息安全而言,止大风于青萍之末是上上策,杭研深入各个细节的研发工作,正是网易产 ...

  3. 浅谈Android 混淆和加固

    混淆: 针对项目代码,代码混淆通常将代码中的各种元素(变量.函数.类名等)改为无意义的名字,使得阅读的人无法通过名称猜测其用途,增大反编译者的理解难度. 虽然代码混淆可以提高反编译的门槛,但是对开发者 ...

  4. Android 第三方加固方案 对比 MD

    常见的第三方加固方案官网介绍 由于安卓APP是基于Java的,所以极容易被破解,一个不经过加固的APP犹如裸奔一样,毫无防备.之前曾有新闻报道,一些专职的APP打包黑产就是专门从各种渠道找到apk,通 ...

  5. 谋哥：App排行榜的秘密

    App在改变世界,改变人们的生活.       如今购物大家都用淘宝.京东,吃饭你会用饭否,看天气预报你用墨迹天气,看视频用优酷.K歌你用唱吧,聊天联系你用微信,看新闻你用今日头条等等.你的生活由你自 ...

  6. App山寨疯狂 爱加密Apk加密平台防破解

    App山寨疯狂 爱加密Apk加密平台防破解,Android系统由于其开源性,眼下已占领全球智能机近80%的市场,远超微软的WP系统和苹果的IOS系统.然而也正是由于开源性,Android盗版App在国 ...

  7. Python爬虫入门教程 42-100 爬取儿歌多多APP数据-手机APP爬虫部分

    1. 儿歌多多APP简单分析 今天是手机APP数据爬取的第一篇案例博客,我找到了一个儿歌多多APP,没有加固,没有加壳,没有加密参数,对新手来说,比较友好,咱就拿它练练手,熟悉一下Fiddler和夜神 ...

  8. Python爬虫入门教程 41-100 Fiddler+夜神模拟器+雷电模拟器配置手机APP爬虫部分

    爬前叨叨 从40篇博客开始,我将逐步讲解一下手机APP的爬虫,关于这部分,我们尽量简化博客内容,在这部分中可能涉及到一些逆向,破解的内容,这部分尽量跳过,毕竟它涉及的东西有点复杂,并且偏离了爬虫体系太 ...

  9. 某地理位置模拟APP从壳流程分析到破解

    工具与环境 Xposed IDA 6.8 JEB 2.2.5 Fiddler2 010Editor NEXUS 5  Android 4.4 好久不玩逆向怕调试器生锈,拿出来磨磨! 高手莫要见笑,仅供 ...

随机推荐

  1. 解决电脑各种 dll 文件丢失问题

    https://jingyan.baidu.com/article/ae97a646f9dbfdbbfc461d6d.html 下载鲁大师,点右上角的 游戏库,然后再点右上角的  修复  ,一键修复即 ...

  2. HDU--2962

    原题链接:http://acm.hdu.edu.cn/showproblem.php?pid=2962 分析:最短路+二分. #include<iostream> #include< ...

  3. Codeforces 717.F Heroes of Making Magic III

    F. Heroes of Making Magic III time limit per test 3 seconds memory limit per test 256 megabytes inpu ...

  4. mysql group_concat方法用法

    目前有三张表: 课程表: course,里面有student_id 学生表:     student,里面有 name 字段 中间表(课程和学生一对多): course_student, 里面有 co ...

  5. python之numpy矩阵库的使用（续）

    本文是对我原先写的python常用序列list.tuples及矩阵库numpy的使用中的numpy矩阵库的使用的补充.结合我个人现在对线性代数的复习进度来不断更博. Section 1:行列式的计算 ...

  6. 解决html设置height：100%无效的问题

    通常我们需要让自己的网页内容能够更好的适配各种屏幕大小,会采用height:100%,但是我们发现问题出来了,height:100%无效,其实解决办法很简单 解决:你只需要在css处添加上html, ...

  7. MySql 插入数据库报错 Incorrect string value: '\xF0\xA0\x86\xA2'

    今天从nginx日志分析搜索关键字,然后把关键字插入到Mysql数据库里,出现如下错误 SQL state [HY000]; error code [1366]; Incorrect string v ...

  8. POJ 2318/2398 叉积性质

    2318 2398 题意:给出n条线将一块区域分成n+1块空间,再给出m个点,询问这些点在哪个空间里. 思路:由于只要求相对位置关系,而对具体位置不关心,那么易使用叉积性质得到相对位置关系(左侧/右侧 ...

  9. Spring Cacheable 注解不缓存null值

    用Cacheable注解时,发现空值,也会被缓存下来.如果我们期望空值不被缓存,可以做如下设置: @Cacheable(key = "#id", unless="#res ...

  10. [php]referer应用--http防盗链技术

    1.防盗链的理解 所谓防盗链是防止其他的网站引用自己网站的资源连接,比如图片.视频等等,但是并不会阻碍从自己网站上享受资源的用户,这就要求能够将其他网站的连接请求阻止 2.防盗链的原理 其实从自己网站 ...