SKINNY加密算法详解(无代码,仅加密)
原作者论文请参考《The SKINNY Family of Block Ciphers and Its Low-Latency Variant MANTIS》
地址为:https://link.springer.com/chapter/10.1007/978-3-662-53008-5_5
代码及资源分析等参见:https://sites.google.com/site/skinnycipher/home
SKINNY 和 AES 类似,都是SPN结构的加密算法。
本文中截图多来自上述论文。
一、整体流程

其中包括5个步骤,分别为字节替换、轮加常数、轮加密钥、行移位、列混淆。
SKINNY有一下几种模式:
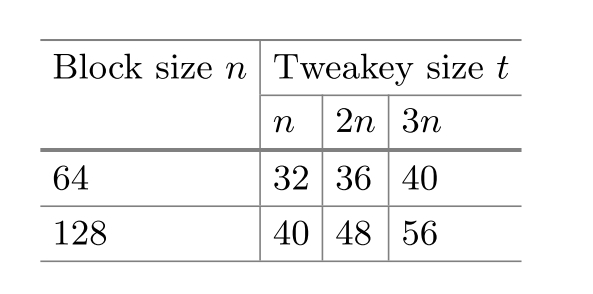
其中,n为明文长度,有64位和128位两种;对于每种明文,密钥有3种形式n/2n/3n,即64/128位、64/128 * 2位、64/128 * 3位;对应的模式下,分别运行32、36、40...轮。
首先,将明文划分为16份,若明文为64位,则每份半个字节;若为128,每份一个字节。
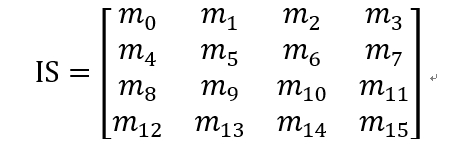
可变长度的密钥为以下形式,tk = tk0 tk1 ... tk16z-1 ,这里 z = 1, 2, 3。令0≤i≤15,当 z = 1 有TK1i = tki,当 z = 2 有TK1i = tk16+i,当 z = 3 有TK1i = tk32+i。
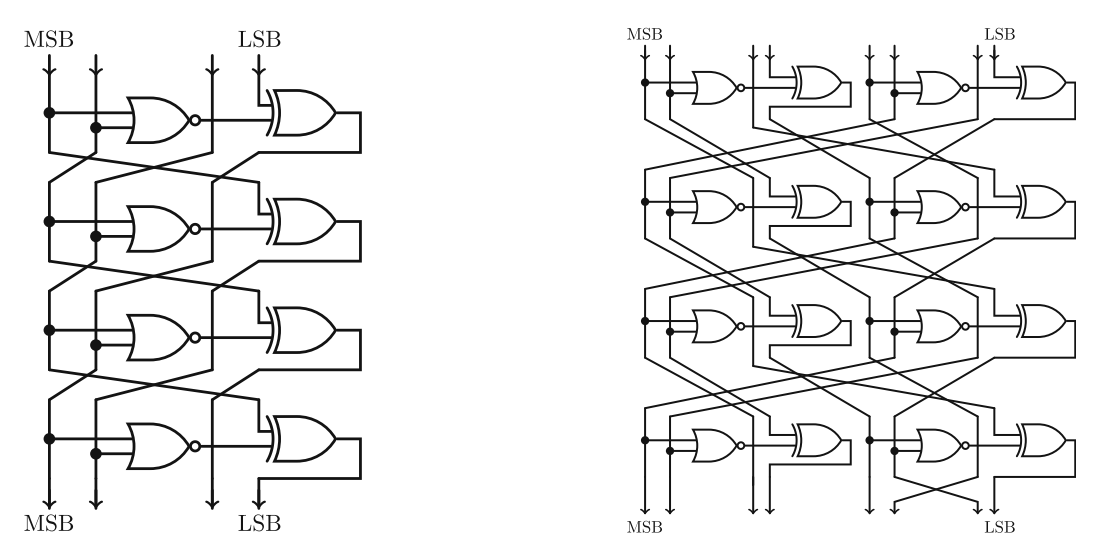
1. 字节替代(Subbyte)
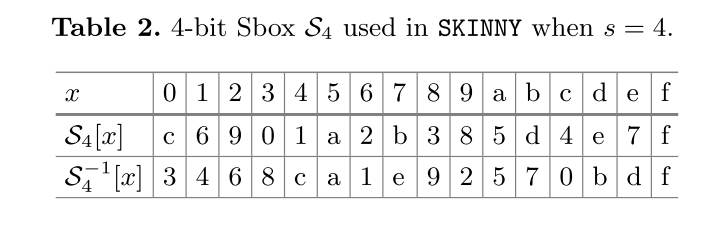
字长有4bit和8bit两种,分别有对应的SBOX,对于4bit形式,有如下SBOX,
上述4-bit SBOX可以用或非门和异或门实现,如下操作:
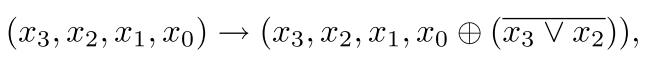
对于4-bit和8-bit S盒,有如下结构:
对于8-bit S盒有以下操作,首先,
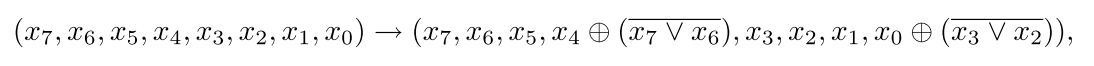
然后进行位置换,

重复以上步骤4次,但是在最后一次时仅对x1和x2置换。
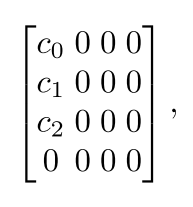
2. 加常数(AddConstants)
6位的线性反馈移位寄存(LFSR)来产生常数,按以下方式更新:
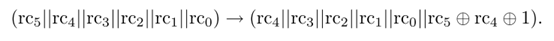
LFSR的初始值为000000,在进行AddConstants操作前,进行更新。如进行第一轮AddConstants操作前,先进行000000→000001。
然后,
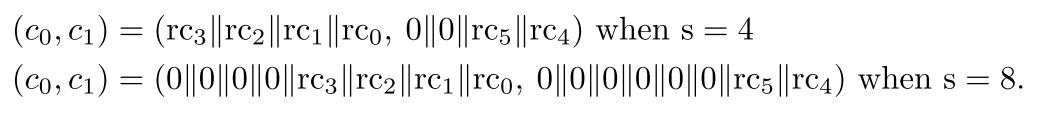
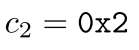
得到矩阵,将此矩阵加到状态矩阵上。
3. 轮密钥加(AddRoundTweakey)
密钥的第一行和第二行和状态矩阵相应的位置异或,对于 i = {0,1} 和 j={0,1,2,3},有以下操作:
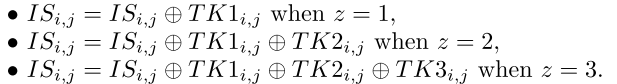
然后将密钥按下图更新:
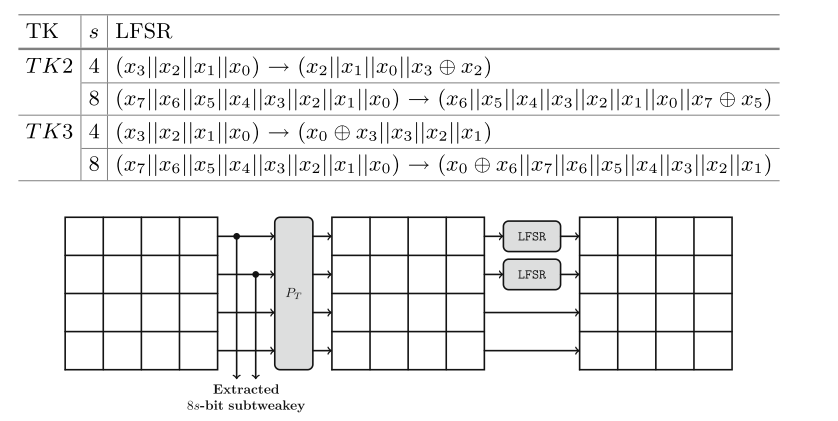
其中,置换函数PT 为:

即(0,...,15)→ (9,15,8,...,5,6,7),其中数字代表密钥矩阵的单元;
4. 行移位(ShiftRows)

矩阵第0行不变,第1行循环右移1个字节,第2行循环右移2个字节,第3行循环右移3个字节,可等效为以下字节置换操作;
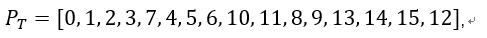
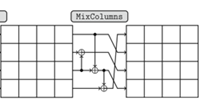
5. 列混淆(MixColumns)
M * IS,其中,
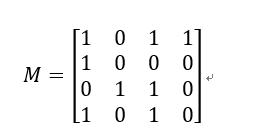
若NSi表示更新后的第i行,Si表示更新前的第i行,参考以上形式,有
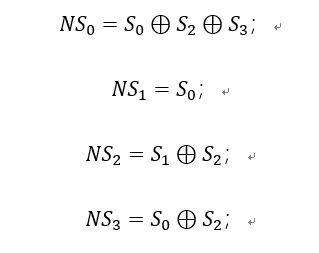
SKINNY加密算法详解(无代码,仅加密)的更多相关文章
- Python - 元组(tuple) 详解 及 代码
元组(tuple) 详解 及 代码 本文地址: http://blog.csdn.net/caroline_wendy/article/details/17290967 元组是存放任意元素集合,不能修 ...
- Python - 字典(dict) 详解 及 代码
字典(dict) 详解 及 代码 本文地址: http://blog.csdn.net/caroline_wendy/article/details/17291329 字典(dict)是表示映射的数据 ...
- 深度学习之卷积神经网络(CNN)详解与代码实现(一)
卷积神经网络(CNN)详解与代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/10430073.html 目 ...
- C#的String.Split 分割字符串用法详解的代码
代码期间,把代码过程经常用的内容做个珍藏,下边代码是关于C#的String.Split 分割字符串用法详解的代码,应该对码农们有些用途. 1) public string[] Split(params ...
- laravel 框架配置404等异常页面的方法详解(代码示例)
本篇文章给大家带来的内容是关于laravel 框架配置404等异常页面的方法详解(代码示例),有一定的参考价值,有需要的朋友可以参考一下,希望对你有所帮助. 在Laravel中所有的异常都由Handl ...
- Android java程序员必备技能,集合与数组中遍历元素,增强for循环的使用详解及代码
Android java程序员必备技能,集合与数组中遍历元素, 增强for循环的使用详解及代码 作者:程序员小冰,CSDN博客:http://blog.csdn.net/qq_21376985 For ...
- .NET DLL 保护措施详解(非混淆加密加壳)
为什么要保护DLL,我就不多说了,各人有各人的理由.总的来说,就是不想核心逻辑泄露及授权验证被破解两大方面的因素.市面上的混淆加密工具对.NET源码保护的效果天差地别,很多网上下到的混淆工具破解版对. ...
- UIWebView用法详解及代码分享
今天我们来详细UIWebView用法.UIWebView是iOS内置的浏览器控件,可以浏览网页.打开文档等 能够加载html/htm.pdf.docx.txt等格式的文件. 用UIWebView我们就 ...
- 【Android 应用开发】Ubuntu 下 Android Studio 开发工具使用详解 (旧版本 | 仅作参考)
. 基本上可以导入项目开始使用了 ... . 作者 : 万境绝尘 转载请注明出处 : http://blog.csdn.net/shulianghan/article/details/21035637 ...
随机推荐
- 洗礼灵魂,修炼python(47)--巩固篇—定义类的方法之@classmethod,@staticmethod
定义类的方法,相信你会说,不就是在class语句下使用def () 就是定义类的方法了嘛,是的,这是定义的方法的一种,而且是最普通的方式 首先,我们已经知道有两种方式: 1.普通方法: 1)与类无关的 ...
- Linux查看服务器配置常用
1. 内存: free:查看内存 total:总共内存 2. 处理器数量: cat /proc/cpuinfo | grep "processor" | wc -l 3.处理器 ...
- python中的一等对象--函数
一等对象 什么是一等对象: 在运行时创建 能赋值给变量或数据结构中的元素 能作为参数传递给函数 能作为函数的返回结果 python中的字符串,列表什么的都是一等对象,但对如果之前只是使用c++.jav ...
- Linux远程访问及控制(SSH)
1.ssh协议:用于远程登录,端口号:22/tcp 配置文件: 1)服务器端口:/etc/ssh/sshd_config 2)客户端 :/etc/ssh/ssh_config 2.服务器监听选项: U ...
- 3.8Python数据处理篇之Numpy系列(八)---Numpy的梯度函数
目录 目录 前言 (一)函数说明 (二)一维数组的应用 (三)多维数组的应用 目录 前言 梯度函数,其中的梯度也就是斜率,反映的是各个数据的变化率.在numpy中只有一个梯度函数. (一)函数说明 ( ...
- LNMP环境搭建详细教程
之前有一篇博客写的是LAMP的环境搭建,今天来详细介绍一下另外一个模式——LNMP=Linux+Nginx+MySQL+PHP. 一.在Linux系统下nginx的安装过程,先到http://ngin ...
- Eclipse中定位当前文件在项目中的位置
点击红色框内的按钮,就能定位当前文件在项目中的位置, 另外, 找到位置后记得再点击一下这个按钮, 要不然每次打开一个文件都会自动定位
- PJ初赛复习日记
PA姑娘的PJ初赛复习日记 by Pleiades_Antares PJ初赛考试马上就要开始了(今年应该是10.13吧?),作为蒟蒻的我们怎么能不复习呢? 众所周知,复习方法有很多很多种-- 比如 ( ...
- 个人技术博客Alpha----Android Studio学习
项目联系: 本次项目我主要负责Android studio的后端,以及游戏文案游戏策划,结果后来事情太散了,Android studio学的不咋地,文案写完还有帮着写一写数据库的插入语句,然后就是跟队 ...
- Apha冲刺! Day2 - 砍柴
Alpha冲刺! Day2 - 砍柴 今日已完成 晨瑶:没做和主项目相关的事情,除了教队友用gitkraken. 昭锡:学习LitePal对数据库进行操作. 永盛:切换 API 管理平台,继续撰写 A ...
