KM算法小结

最近有一个需求，主要内容如下：

APP一般刷新一次，会返回6个Item（6可能会变），每个Item都要展示一个广告，其中每个Item会发送一个请求，返回的结果是一个广告数组，比如[ad1, ad2, ad3....]，不同ad含有自己的eCPM值（数值），在同一个广告数组里面，不同ad的eCPM值可以认为不会相同，但是在不同广告数组之间，可能会有相同的Ad。现在的需求是需要在6个广告数组中每一个取出一个Ad，让eCPM的和最大，但是Ad不能重复。

思考：

这道题不能简单的在每个数组内部进行排序，然后每个数组取最大值，这样的话，很可能两个数组选了同一个Ad，这在题目中是不被允许的。开始我的思路是，先针对每个数组进行从大到小的排序，如果多个数组第一个是同一个Ad，那么接着看第二个元素，第一个元素就选第二个小的那个，以此类推。但是这样室友问题的，会陷入局部最优，两个数组还好说，要是多个的话，之前你之所以选第二个元素小的那个的第一个元素，是因为你想用到第二个比较大的元素，但是针对多个，就不一定能用到了，因为你是通过多个比较出来的。

这里介绍一个算法，KM算法，可以参考：

http://www.cnblogs.com/wenruo/p/5264235.html

通过一个例子生动形象：

现在有N男N女，有些男生和女生之间互相有好感，我们将其好感程度定义为好感度，我们希望把他们两两配对，并且最后希望好感度和最大。

怎么选择最优的配对方法呢？

首先，每个女生会有一个期望值，就是与她有好感度的男生中最大的好感度。男生呢，期望值为0，就是……只要有一个妹子就可以啦，不挑~~

这样，我们把每个人的期望值标出来。

接下来，开始配对。

配对方法：

我们从第一个女生开始，分别为每一个女生找对象。

每次都从第一个男生开始，选择一个男生，使男女两人的期望和要等于两人之间的好感度。

注意：每一轮匹配，每个男生只会被尝试匹配一次！

具体匹配过程：

==============为女1找对象===============

（此时无人配对成功）

根据 “男女两人的期望和要等于两人之间的好感度”的规则

女1-男1：4+0 != 3

女1-男3：4+0 == 4

所以女1选择了男3

女1找对象成功

==============为女1找对象成功============

==============为女2找对象===============

（此时女1—男3）

根据配对原则，女2选择男3

男3有主女1，女1尝试换人

我们尝试让女1去找别人

尝试失败

为女2找对象失败！

==============为女2找对象失败============

这一轮参与匹配的人有：女1，女2，男3。

怎么办？？？很容易想到的，这两个女生只能降低一下期望值了，降低多少呢？

这轮

比如：女1选择男1，期望值要降低1。 女2选择男1，期望值要降低1。 女2选择男2，期望值要降低2。

于是，只要期望值降低1，就有妹子可能选择其他人。所以妹子们的期望值要降低1点。

同时，刚才被抢的男生此时非常得意，因为有妹子来抢他，于是他的期望值提高了1点（就是同妹子们降低的期望值相同）。

于是期望值变成这样（当然，不参与刚才匹配过程的人期望值不变）

==============继续为女2找对象=============

（此时女1—男3）

女2选择了男1

男1还没有被配对

女2找对象成功！

==============为女2找对象成功=============

==============为女3找对象===============

（此时女1—男3，女2-男1）

女3没有可以配对的男生……

女3找对象失败

==============为女3找对象失败============

此轮只有女3参与匹配

此时应该为女3降低期望值

降低期望值1的时候，女3-男3可以配对，所以女3降低期望值1

==============继续为女3找对象============

（此时女1—男3， 女2-男1）

女3相中了男3

此时男3已经有主女1，于是女1尝试换人

女1选择男1

而男1也已经有主女2，女2尝试换人

前面说过，每一轮匹配每个男生只被匹配一次

所以女2换人失败

女3找对象再次失败

==============为女3找对象失败============

这一轮匹配相关人员：女1，女2，女3，男1，男3

此时，只要女2降低1点期望值，就能换到男2

（前面提过 只要任意一个女生能换到任意一个没有被选择过的男生所需要降低的最小值）

我们把相应人员期望值改变一下

==============还是为女3找对象============

（此时女1—男3， 女2-男1）

女3选择了男3

男3有主女1，女1尝试换人

女1换到了男1

男1已经有主女2，女2尝试换人

女2换人男2

男2无主，匹配成功！！！

==============为女3找对象成功=============

匹配成功！！！撒花~~

到此匹配全部结束

此时

女1-男1，女2-男2，女3-男3

好感度和为最大：9

知道了这个算法以后，我们的问题怎么转化成该算法呢？在上面这个例子中，我们的左右两侧的节点个数是相同的，但是该算法针对左右两侧节点个数不同的情况同样受用，其实就可以假想为，节点连线边值为0。

在本题中，我们的左侧就是Item1到Item6，一共6个，右侧是6个广告数组中出现的所有广告Ad，我们要找的就是唯一匹配。初始化的时候，如果是Item1，它的广告数组比方是Ad1，Ad5，Ad8，这三个Ad的eCPM分别是3，6，8，那么连线的权重就是3，6，8，和其他广告连线的权重就是0。

因为我们项目是Go开发的，这里我就直接上Go的代码了，其实很好看懂。

package main

import "fmt"

const MAX = 100
const INT_MAX = int(^uint(0) >> 1)
const INT_MIN = ^INT_MAX
//const INT_MAX = 1061109567
//const INT_MIN = -1061109567
var sx []bool //记录寻找增广路时点集x，y里的点是否搜索过
var sy []bool
var match []int //match[i]记录y[i]与x[match[i]]相对应
var weight [][]int
var Cx []int
var Cy []int

func search_path(u int) bool {          //给x[u]找匹配,这个过程和匈牙利匹配是一样的
    sx[u] = true
    for v := 0; v < len(weight[0]); v++ {
        if !sy[v] && Cx[u] + Cy[v] == weight[u][v] {
            sy[v] = true
            if match[v] == -1 || search_path(match[v]) {  //如果第v个y点还没被占，或者第v个y点还可以找到其他可搭配的x点
                match[v] = u
                return true
            }
        }
    }
    return false
}

//weight是权重
func Kuhn_Munkras(max_weight bool) int {
    //如果求最小匹配，则要将边权取反
    if !max_weight {
        for i := 0; i < len(weight); i++ {
            for j := 0; j < len(weight[0]); j++ {
                weight[i][j] = -weight[i][j]
            }
        }
    }

    //初始化顶标，Cx[i]设置为max(weight[i][j] | j=0,..,n-1 ), Cy[i]=0;
    //Cy的顶标都是0
    for i := 0; i < len(Cx); i++ {
        Cx[i] = INT_MIN
        for j := 0; j < len(weight[0]); j++ {
            if Cx[i] < weight[i][j] {
                Cx[i] = weight[i][j]
            }
        }
    }
    fmt.Println(Cx, Cy)
    for i := 0; i < len(match); i++ {
        match[i] = -1
    }

    //不断修改顶标，直到找到完备匹配或完美匹配
    for u := 0; u < len(weight); u++ {   //为x里的每一个点找匹配
        for {
            for index,_ := range sx {
                sx[index] = false
            }
            for index,_ := range sy{
                sy[index] = false
            }
            if search_path(u) {//x[u]在相等子图找到了匹配,继续为下一个点找匹配
                break
            }

            //如果在相等子图里没有找到匹配，就修改顶标，直到找到匹配为止
            //首先找到修改顶标时的增量inc, min(Cx[i] + Cy [i] - weight[i][j],inc);,Cx[i]为搜索过的点，Cy[i]是未搜索过的点,因为现在是要给u找匹配，所以只需要修改找的过程中搜索过的点，增加有可能对u有帮助的边
            inc := INT_MAX
            for i :=0; i < len(weight); i++ {
                if sx[i] {
                    for j := 0;j < len(weight[0]); j++ {
                        if !sy[j] && (Cx[i] + Cy[j] - weight[i][j]) < inc {
                            inc = Cx[i] + Cy[j] - weight[i][j]
                        }
                    }
                }
            }

            //找不到可以加入的边，返回失败（即找不到完美匹配）
            if inc == INT_MAX {
                return -1
            }

            //找到增量后修改顶标，因为sx[i]与sy[j]都为真，则必然符合Cx[i] + Cy [j] =weight[i][j]，然后将Cx[i]减inc，Cy[j]加inc不会改变等式，但是原来Cx[i] + Cy [j] ！=weight[i][j]即sx[i]与sy[j]最多一个为真，Cx[i] + Cy [j] 就会发生改变，从而符合等式，边也就加入到相等子图中
            for i := 0; i < len(weight); i++ {
                if sx[i] { //如果点x在S集合里
                    Cx[i] -= inc
                }
            }
            for j := 0; j < len(weight[0]); j++ {
                if(sy[j]){//如果点y在T集合里
                    Cy[j] += inc
                }
            }
        }

    }
    sum := 0;
    for i := 0; i < len(weight[0]); i++ {
        if match[i] > -1 {
            sum += weight[match[i]][i]
        }
    }

    if !max_weight {
        sum = -sum
        return sum
    }
    return sum
}

func main() {
    sx = make([]bool, 3)
    sy = make([]bool, 3)
    match = make([]int, 3)
    //weight = append(weight, []int{3, 0, 4, 1})
    //weight = append(weight, []int{2, 1, 3, 1})
    //weight = append(weight, []int{0, 0, 5, 1})
    weight = [][]int{
        {3, 0, 4},
        {2, 1, 3},
        {0, 0, 5},
    }

    Cx = make([]int, 3)
    Cy = make([]int, 3)

    sum := Kuhn_Munkras(true)
    fmt.Println(sum)

    fmt.Println(match)
}

运行代码：

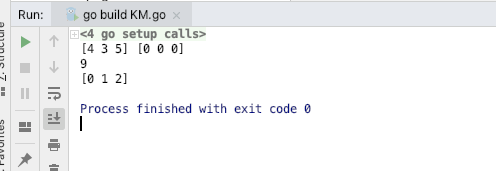
代码中都有注释，就是之前例子中的数据，可以对照着看。

应魏印福要求，我把转换二分图的过程，以及构造生成数组的过程也写出来了，如下：

package main

import (
    "fmt"
    "math/rand"
    "sort"
)

const MAX = 100
const INT_MAX = int(^uint(0) >> 1)
const INT_MIN = ^INT_MAX
//const INT_MAX = 1061109567
//const INT_MIN = -1061109567
var sx []bool //记录寻找增广路时点集x，y里的点是否搜索过
var sy []bool
var match []int //match[i]记录y[i]与x[match[i]]相对应
var weight [][]int
var Cx []int
var Cy []int

func search_path(u int) bool {          //给x[u]找匹配,这个过程和匈牙利匹配是一样的
    sx[u] = true
    for v := 0; v < len(weight[0]); v++ {
        if !sy[v] && Cx[u] + Cy[v] == weight[u][v] {
            sy[v] = true
            if match[v] == -1 || search_path(match[v]) {  //如果第v个y点还没被占，或者第v个y点还可以找到其他可搭配的x点
                match[v] = u
                return true
            }
        }
    }
    return false
}

//weight是权重
func Kuhn_Munkras(max_weight bool) int {
    //如果求最小匹配，则要将边权取反
    if !max_weight {
        for i := 0; i < len(weight); i++ {
            for j := 0; j < len(weight[0]); j++ {
                weight[i][j] = -weight[i][j]
            }
        }
    }

    //初始化顶标，Cx[i]设置为max(weight[i][j] | j=0,..,n-1 ), Cy[i]=0;
    //Cy的顶标都是0
    for i := 0; i < len(Cx); i++ {
        Cx[i] = INT_MIN
        for j := 0; j < len(weight[0]); j++ {
            if Cx[i] < weight[i][j] {
                Cx[i] = weight[i][j]
            }
        }
    }
    //fmt.Println(Cx, Cy)
    for i := 0; i < len(match); i++ {
        match[i] = -1
    }

    //不断修改顶标，直到找到完备匹配或完美匹配
    for u := 0; u < len(weight); u++ {   //为x里的每一个点找匹配
        for {
            for index,_ := range sx {
                sx[index] = false
            }
            for index,_ := range sy{
                sy[index] = false
            }
            if search_path(u) {//x[u]在相等子图找到了匹配,继续为下一个点找匹配
                break
            }

            //如果在相等子图里没有找到匹配，就修改顶标，直到找到匹配为止
            //首先找到修改顶标时的增量inc, min(Cx[i] + Cy [i] - weight[i][j],inc);,Cx[i]为搜索过的点，Cy[i]是未搜索过的点,因为现在是要给u找匹配，所以只需要修改找的过程中搜索过的点，增加有可能对u有帮助的边
            inc := INT_MAX
            for i :=0; i < len(weight); i++ {
                if sx[i] {
                    for j := 0;j < len(weight[0]); j++ {
                        if !sy[j] && (Cx[i] + Cy[j] - weight[i][j]) < inc {
                            inc = Cx[i] + Cy[j] - weight[i][j]
                        }
                    }
                }
            }

            //找不到可以加入的边，返回失败（即找不到完美匹配）
            if inc == INT_MAX {
                return -1
            }

            //找到增量后修改顶标，因为sx[i]与sy[j]都为真，则必然符合Cx[i] + Cy [j] =weight[i][j]，然后将Cx[i]减inc，Cy[j]加inc不会改变等式，但是原来Cx[i] + Cy [j] ！=weight[i][j]即sx[i]与sy[j]最多一个为真，Cx[i] + Cy [j] 就会发生改变，从而符合等式，边也就加入到相等子图中
            for i := 0; i < len(weight); i++ {
                if sx[i] { //如果点x在S集合里
                    Cx[i] -= inc
                }
            }
            for j := 0; j < len(weight[0]); j++ {
                if(sy[j]){//如果点y在T集合里
                    Cy[j] += inc
                }
            }
        }

    }
    sum := 0;
    for i := 0; i < len(weight[0]); i++ {
        if match[i] > -1 {
            sum += weight[match[i]][i]
        }
    }

    if !max_weight {
        sum = -sum
        return sum
    }
    return sum
}

/**
生成器
第一个参数是itemNum的数量，也是数组的个数，第二个参数是每个数组的元素个数
 */
func generater(itemNum int, num int) [][]int {
    itemList := make([][]int, 0)
    for n := 0; n < itemNum; n++ {
        list := make([]int, 0)
        for i := 0; i < num; i++ {
            rand := randInt(1, 20)
            for find(rand, list){
                rand = randInt(1, 20)
            }
            list = append(list, rand)
            sort.Sort(sort.Reverse(sort.IntSlice(list)))
        }
        itemList = append(itemList, list)
    }
    return itemList
}
//查找切片中是否存在某个数
func find(target int, list []int) bool {
    for _, num := range list {
        if num == target {
            return true
        }
    }
    return false
}

func randInt(min int, max int) int {
    return min + rand.Intn(max - min)
}

/**
初始化方法
 */
func initMethod() {
    ints := generater(6, 8)

    Cx = make([]int, len(ints))
    CyList := []int{}
    for i := 0; i < len(ints); i++ {
        for j := 0; j < len(ints[0]); j++ {
            CyList = append(CyList, ints[i][j])
        }
    }
    CyList = RemoveRepByMap(CyList)
    Cy = make([]int, len(CyList))

    //fmt.Println(len(ints))
    //fmt.Println(CyList)
    sx = make([]bool, len(ints))
    sy = make([]bool, len(CyList))
    match = make([]int, len(CyList))
    //weight = append(weight, []int{3, 0, 4, 1})
    //weight = append(weight, []int{2, 1, 3, 1})
    //weight = append(weight, []int{0, 0, 5, 1})
    weight = make([][]int, 0)
    for i := 0; i < len(ints); i++ {
        weightlist := make([]int, len(CyList))
        for j := 0; j < len(CyList); j++ {
            if find(CyList[j], ints[i]) {
                weightlist[j] = CyList[j]
            } else {
                weightlist[j] = 0
            }
        }
        weight = append(weight, weightlist)
    }
    fmt.Println("weight:", weight)
}

// 通过map主键唯一的特性过滤重复元素
func RemoveRepByMap(slc []int) []int {
    result := []int{}
    tempMap := map[int]byte{}  // 存放不重复主键
    for _, e := range slc {
        l := len(tempMap)
        tempMap[e] = 0
        if len(tempMap) != l{  // 加入map后，map长度变化，则元素不重复
            result = append(result, e)
        }
    }
    return result
}

func main() {
    initMethod()

    sum := Kuhn_Munkras(true)
    fmt.Println("sum:", sum)

    fmt.Println("match:", match)
}

参考

https://blog.csdn.net/li13168690086/article/details/81557890

https://blog.csdn.net/x_y_q_/article/details/51927054

https://www.cnblogs.com/xiaochaoqun/p/7207658.html

http://www.cnblogs.com/wenruo/p/5264235.html