.NET如何写正确的“抽奖”——打乱数组算法

.NET如何写正确的“抽奖”——数组乱序算法

数组乱序算法常用于抽奖等生成临时数据操作。就拿年会抽奖来说，如果你的算法有任何瑕疵，造成了任何不公平，在年会现场code review时，搞不好不能活着走出去。

这个算法听起来很简单，简单到有时会拿它做面试题去考候选人，但它实际又很不容易，因为细节很重要，稍不留神就错了。

首先来看正确的做法：

T[] ShuffleCopy<T>(IEnumerable<T> data, Random r)
{
    var arr = data.ToArray();

    for (var i = arr.Length - 1; i > 0; --i)
    {
        int randomIndex = r.Next(i + 1);

        T temp = arr[i];
        arr[i] = arr[randomIndex];
        arr[randomIndex] = temp;
    }

    return arr;
}

可以在LINQPad 6中，使用如下代码，测试随机打乱0-10的数列，进行50万条次模拟统计：

int[] Measure(int n, int maxTime)
{
	var data = Enumerable.Range(0, n);
	var sum = new int[n];

	var r = new Random();
	for (var times = 0; times < maxTime; ++times)
	{
		var result = ShuffleCopy(data, r);
		for (var i = 0; i < n; ++i)
		{
			sum[i] += result[i] != i ? 1 : 0;
		}
	}

	return sum;
}

然后可以使用LINQPad特有的报表函数，将数据展示为图表：

Util.Chart(
	Measure(10, 50_0000).Select((v, i) => new { X = i, Y = v}),
	x => x.X, y => y.Y, Util.SeriesType.Bar
	).Dump();

运行效果如下（记住这是正确的示例）：

可见50万次测试中，曲线基本平稳，0-10的分布基本一致，符合统计学上的概率相等。

再来看看如果未做任何排序的代码：

T[] ShuffleCopy<T>(IEnumerable<T> data, Random r) => data.ToArray();

曲线：

记住这两条曲线，它们将作为我们的参考曲线。

不然呢？

其实正确的代码每一个标点符号都不能错，下面我将演示一些错误的示例

错误示例1

多年前我看到某些年会抽奖中使用了代码（使用JavaScript、错误示例)：

[0,1,2,3,4,5,6,7,8,9].sort((a, b) => Math.random() - 0.5)
// 或者
[0,1,2,3,4,5,6,7,8,9].sort((a, b) => Math.random() - Math.random())

返回结果如下：

(10) [8, 4, 3, 6, 2, 1, 7, 9, 5, 0]

看起来“挺”正常的，数据确实被打乱了，这些代码在C#中也能轻易写出来：

T[] ShuffleCopy<T>(IEnumerable<T> data, Random r) =>
	data.OrderBy(v => r.NextDouble() < 0.5).ToArray();

50万条数据统计结果如下：

可见，排在两端的数字几乎没多大变化，如果用于公司年会抽奖，那么排在前面的人将有巨大的优势。

对比一下，如果在公司年会抽奖现场，大家Code Review时在这时“揭竿而起”，是不是很正常？

为什么会这样？

因为排序算法的本质是不停地比较两个值，每个值都会比较不止一次。因此要求比较的值必须是稳定的，在此例中明显不是。要获得稳定的结果，需要将随机数固定下来，像这样：

T[] ShuffleCopy<T>(IEnumerable<T> data, Random r) => data
	.Select(v => new { Random = r.NextDouble(), Value = v})
	.OrderBy(v => v.Random)
	.Select(x => x.Value)
	.ToArray();

此时结果如下（正确）：

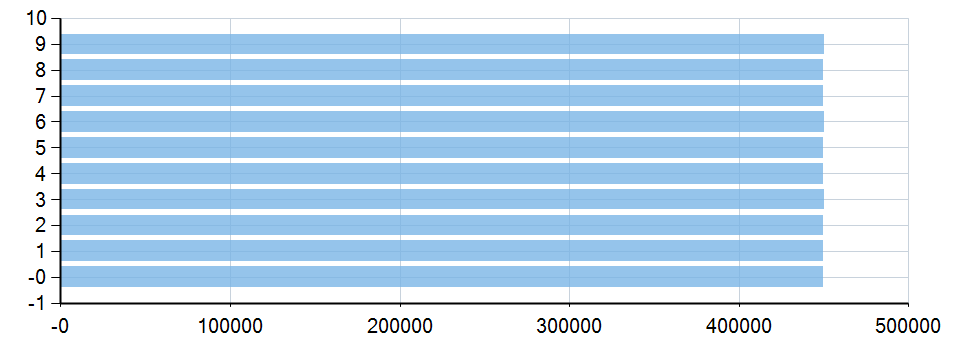
这种算法虽然正确，但它消耗了过多的内存，时间复杂度为整个排序的复杂度，即O(N logN)。

乱个序而已，肯定有更好的算法。

错误示例2

如果将所有值遍历一次，将当前位置的值与随机位置的值进行交换，是不是也一样可以精准打乱一个数组呢？

试试吧，按照这个想法，代码可写出如下：

T[] ShuffleCopy<T>(IEnumerable<T> data, Random r)
{
	var arr = data.ToArray();

	for (var i = 0; i < arr.Length; ++i)
	{
		int randomIndex = r.Next(arr.Length);

		T temp = arr[i];
		arr[i] = arr[randomIndex];
		arr[randomIndex] = temp;
	}

	return arr;
}

运行结果如下：

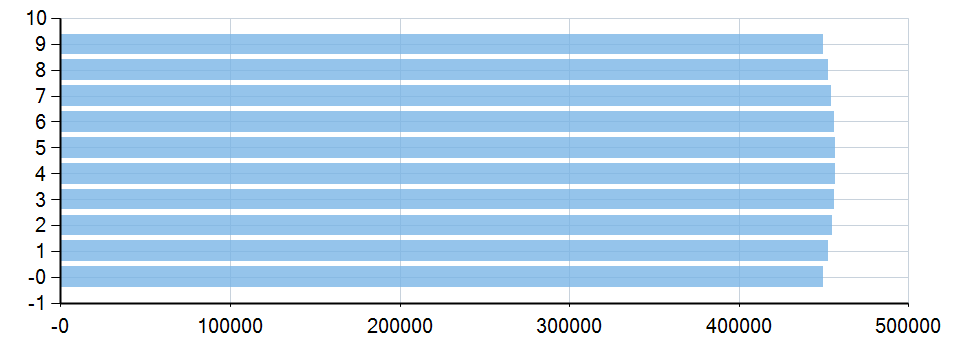
有一点点不均匀，我可以保证这不是误差，因为多次测试结果完全一样，咱们拿数据说话，通过以下代码，可以算出所有值的变化比例：

Measure(10, 50_0000).Select(x => (x / 50_0000.0).ToString("P2")).Dump();

结果如下：

0 90.00%
1 90.54%
2 90.97%
3 91.29%
4 91.41%
5 91.38%
6 91.31%
7 90.97%
8 90.60%
9 90.01%

按道理每个数字偏离本值比例应该是90.00%的样子，本代码中最高偏离值高了1.41%，作为对比，可以看看正确示例的偏离比例数据：

0 90.02%
1 90.05%
2 90.04%
3 89.98%
4 90.05%
5 90.04%
6 90.07%
7 90.03%
8 89.97%
9 90.02%

可见最大误差不超过0.05%，相比高达1%的误差，这一定是有问题的。

其实问题在于随机数允许移动多次，如果出现多次随机，可能最终的值就不随机了，可以见这个示例，如果一个窗口使用这样的方式随机画点：坐标x两个随机数相加、坐标y仅一个随机数，示例代码如下：

// 安装NuGet包：FlysEngine.Desktop
using var form = new RenderWindow();
var r = new Random();
var points = Enumerable.Range(0, 10000)
	.Select(x => (x: r.NextDouble() + r.NextDouble(), y: r.NextDouble()))
	.ToArray();
form.Draw += (o, ctx) =>
{
	ctx.Clear(Color.CornflowerBlue);
	foreach (var p in points)
	{
		ctx.FillRectangle(new RectangleF(
			(float)p.x / 2 * ctx.Size.Width,
			(float)p.y * ctx.Size.Width,
			ctx.Size.Width / 100, ctx.Size.Height / 100), form.XResource.GetColor(Color.Black));
	}
};
RenderLoop.Run(form, () => form.Render(0, PresentFlags.None));

那么画出来的点可能是这个样子：

可见，1万条数据，x坐标两个随机数相加之后，即使下方代码中除以2了，结果已经全部偏向中间值了（和本例代码效果一样），而只使用一次的y坐标，随机程度正常。想想也能知道，就像扔色子一样，两次扔色子平均是6的机率远比平均是3的机率低。

因此可以得出一个结论：随机函数不能随意叠加。

错误示例3

如何每个位置的点只交换一次呢？没错，我们可以倒着写这个函数，首先来看这样的代码：

T[] ShuffleCopy<T>(IEnumerable<T> data, Random r)
{
	var arr = data.ToArray();

	for (var i = arr.Length - 1; i > 0; --i)
	{
		int randomIndex = r.Next(i);

		T temp = arr[i];
		arr[i] = arr[randomIndex];
		arr[randomIndex] = temp;
	}

	return arr;
}

注意循环终止条件是i > 0，而不是直接遍历的i >= 0，因为r.Next(i)的返回值一定是小于i的，用>=0没有意义，首先来看看结果：

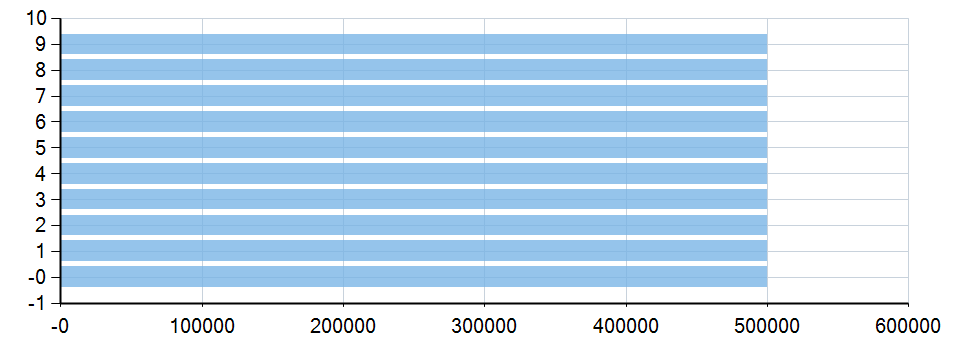
用这个算法，每个数字出来都一定不是它自己本身，这合理吗？听起来感觉也合理，但真的如此吗？

假设某公司年会使用该算法抽奖，那结论就是第一个人不可能中奖，如果恰好你正好是抽奖名单列表的第一个人，你能接受吗？

据说当年二战时期德国的通讯加密算法，就是因为加密之前一定和原先的数据不一样，导致安全性大大降低，被英国破解的。

这个问题在于算法没允许和数字和自己进行交换，只需将r.Next(i)改成r.Next(i + 1)，问题即可解决。

总结

所以先回顾一下文章最初算法：

T[] ShuffleCopy<T>(IEnumerable<T> data, Random r)
{
    var arr = data.ToArray();

    for (var i = arr.Length - 1; i > 0; --i)
    {
        int randomIndex = r.Next(i + 1);

        T temp = arr[i];
        arr[i] = arr[randomIndex];
        arr[randomIndex] = temp;
    }

    return arr;
}

然后重新体会一下它性感的测试数据（10条数据，标准的90%）：

只有写完很多个不正确的版本，才能体会出写出正确的代码，每一个标点符号都很重要的感觉。

喜欢的朋友 请关注我的微信公众号：【DotNet骚操作】