洛谷P1283 平板涂色 &&一本通1445：平板涂色

题目描述

CE数码公司开发了一种名为自动涂色机（APM）的产品。它能用预定的颜色给一块由不同尺寸且互不覆盖的矩形构成的平板涂色。

为了涂色，APM需要使用一组刷子。每个刷子涂一种不同的颜色C。APM拿起一把有颜色C的刷子，并给所有颜色为C且符合下面限制的矩形涂色：



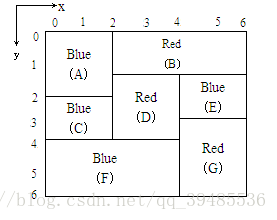
为了避免颜料渗漏使颜色混合，一个矩形只能在所有紧靠它上方的矩形涂色后，才能涂色。例如图中矩形F必须在C和D涂色后才能涂色。注意，每一个矩形必须立刻涂满，不能只涂一部分。

写一个程序求一个使APM拿起刷子次数最少的涂色方案。注意，如果一把刷子被拿起超过一次，则每一次都必须记入总数中。

【输入】

第一行为矩形的个数N。下面有N行描述了N个矩形。每个矩形有5个整数描述，左上角的y坐标和x坐标，右下角的y坐标和x坐标，以及预定颜色。

颜色号为1到20的整数。

平板的左上角坐标总是(0, 0)。

坐标的范围是0..99。N小于16。

【输出】

拿起刷子的最少次数。

【输入样例】

7

0 0 2 2 1

0 2 1 6 2

2 0 4 2 1

1 2 4 4 2

1 4 3 6 1

4 0 6 4 1

3 4 6 6 2

【输出样例】

3

蒟蒻看到这题，先是mengbi，表示不会DP，只能搜索（+剪枝）

这数据竟然过了(n<16)

搜索思路

读入数据，统计颜色，然后每个颜色都试一遍，即把该颜色的且能涂的砖涂上。

下一次涂色不能涂上次涂过的色。涂完了记录结果

这不会超时吗老铁

为了不超时，加了两个剪枝

最优化剪枝：当前涂色次数大于等于当前答案，直接退出（这个好理解吧）

可行性剪枝：如果当前一个砖都没有涂到，直接退出（如果接着搜，会多一个次数，可能还会死循环，，，）

至于判断该砖是否能涂，先预处理，把紧邻该砖上方的砖用数组记录下来，再判断那些砖是否被涂

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<string>
#include<algorithm>
#include<iomanip>
#include<cstdlib>
#include<queue>
#include<map>
#include<set>
#include<stack>
#include<vector>
#define ll long long
using namespace std;
inline int read()
{
   int s=0,w=1;
   char ch=getchar();
   while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
   while(isdigit(ch)) s=s*10+ch-'0',ch=getchar();
   return s*w;
}
struct lbq  //结构体 a1b1 该砖左上角坐标 a2b2 右下角坐标 x 颜色
{
    int a1,b1,a2,b2,x;
}a[20];
int ccmp(lbq a,lbq b)
{
    if(a.a1!=b.a1) return a.a1<b.a1;
    return a.b1<b.b1;
}
bool d=false;
int de[20];//de数组表示是否有该颜色
int n,m,ans=999,b[20],fk[20][20]; //b数组代表该砖是否被涂
bool OK(int o)
{
    for(int i=1;i<=n;i++)
        if(fk[o][i]&&!b[i]) return false; //如果i砖下面紧邻o，但i没涂过，返回false
    return true;
}
void dfs(int o,int pq,int xx)//o 涂色次数 pq 涂过颜色的砖 xx 上次涂的颜色
{
    if(o>=ans) return;//当前涂色次数大于等于当前答案，直接退出
    if(pq==n)//涂完了，记录答案
    {
        ans=o;
        return;
    }
    for(int i=1;i<=m;i++)//枚举颜色
    {
        int oj=0;//代表现在用这个颜色涂的砖数
        if(i!=xx&&de[i])//如果有这个颜色，并且这种颜色上次没用过
        {
            for(int j=1;j<=n;j++) //涂色
                if(!b[j]&&a[j].x==i&&OK(j))
				//如果没涂过该砖，并且能涂
                    b[j]=1,oj++;
                else
				if(b[j]&&a[j].x==i)
				b[j]++;
           if(oj>0)
		   dfs(o+1,pq+oj,i);//如果涂了砖，进行下一步
           for(int j=n;j>=1;j--)//回溯一步
                if(b[j]==1&&a[j].x==i&&OK(j))
                    b[j]=0,oj--;
                else
				if(b[j]>1&&a[j].x==i)
				b[j]--;
        }
    }
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
        a[i].a1=read(),a[i].b1=read(),a[i].a2=read(),a[i].b2=read(),a[i].x=read(),
        a[i].a1++,a[i].b1++,de[a[i].x]++;//记录颜色
    for(int i=1;i<=20;i++)
	if(de[i])
	m=i; //求最大颜色编号
    sort(a+1,a+n+1,ccmp);//按左上角坐标大小从小到大排序（先考虑纵，再考虑横）
    for(int i=2;i<=n;i++)
        for(int j=i-1;j>=1;j--)//fk[i][j]表示第i个砖是否紧邻上方第j个砖
            if(a[i].a1==a[j].a2+1&&((a[i].b1>=a[j].b1&&a[i].b1<=a[j].b2)||(a[i].b2>=a[j].b1&&a[i].b2<=a[j].b2)))
                fk[i][j]=1;//如果i砖的最上面紧邻j砖最下面，且两砖横坐标有重叠，即j砖为i砖紧邻上面的砖
    dfs(0,0,0);
    printf("%d",ans);//结果
    return 0;
}