NOIP模拟赛18 皇帝的烦恼O(∩_∩)O 二分+DP

题目描述

经过多年的杀戮，秦皇终于统一了中国。为了抵御外来的侵略，他准备在国土边境安置n名将军。不幸的是这n名将军羽翼渐丰，开始展露他们的狼子野心了。他们拒绝述职、拒绝接受皇帝的圣旨。

秦皇已经准备好了秘密处决这些无礼的边防大将。

不过为防兵变，他决定先授予这些将军一些勋章，为自己赢得战略时间。将军们听说他们即将被授予勋章都很开心，他们纷纷上书表示感谢。第i个将军要求得到ai枚不同颜色的勋章。但是这些将军都很傲气，如果两个相邻的将军拥有颜色相同的勋章他们就会认为皇帝不尊重他们，会立即造反（编号为i的将军和编号为i+1的将军相邻；因为他们驻扎的边境可以类似看成一个圆形，所以编号1和编号n的将军也相邻）。

皇帝不得不满足每个将军的要求，但对他们的飞扬跋扈感到很气愤。于是皇帝决定铸造尽量少种类的勋章来满足这些狂妄者的要求。请问他至少要铸造多少种颜色的勋章？

输入格式

第一行有一个整数n(1<=n<=20000)。

接下来n行每行一个整数ai，表示第i个将军要求得到多少种勋章。(1<=ai<=100000)

输出格式

输出一个整数，即最少需要多少种勋章。

输入输出样例

输入 #1复制

4
2 2 1 1

输出 #1复制

    4

一句话题意：

• 有N个将军，每人想要一定量的勋章，他们排成一个环，每个人和他相邻的两个人有的勋章都不能一样，问总共要造多少个勋章

考试时没时间时骗分的方法

• 这题第一眼会产生两种方法：一个事二分加乱搞，另一个就是贪心+撞运气，在完全没有思路或者没时间的时候第二种方法加一个对拍就是一个好的方法；
• 这题感觉考试时不少人都在贪，廖半仙和ZWJDD不知道咋搞的炸了，可为啥我的贪心没有脑子，还有55分？？？
• 感觉凭感觉会觉得答案就是A[i]+A[i+1]的最大值，至于为什么证明后面会有。
• 然后交上去，也确实啥也没判，也没分奇偶，还有分，还怪多。。。

考试时在时间很多/第三题一点也不会时（就像这次）搞的正解

• 正解感觉也很神奇，对于考试时是怎么想到的，我也不知道，感觉什么都不能用，那就DP吧。。。
• 先举几个栗子：

                   

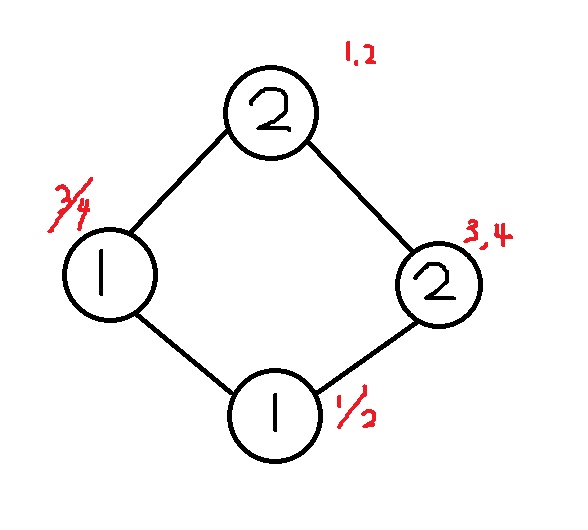
样例：巨水，偶数个，很简单可得有四个                              5个人，没人都要一个，可得要三个                     三个人，每人要一个，共要3个

• 一个大胆的想法偶数时，很简单，自己和相邻的一个人取一个最大值，因为是偶数个，可以将奇数分为一组，偶数分为一组，让他们没有勋章是一样的，很容易可以想到。
• 在看后面两个奇数时，发现没有什么明显的规律，那就很明显的发现，这题难就难在奇数，任何奇数都可以拆成2*N+1的形式，那最后的那个1怎么办？

奇数时判断的方法（重点）：

• 重点就在于怎么判断最后一个和第一个（废话。。。）
• 这题贪心果断排除，什么其他高级算法也想不到，那就写DP吧。。。感觉除了长得清奇一点还是很好想的。
• maxn【i】：表示在前（i-1）个均不冲突时，第i个点与第1个点冲突的最大值
• mx【i】：表示在前（i-1）个均不冲突时，第i个点与第1个点冲突的最小值
• 方程式1：maxn【i】=min ( a [ i ]  , a [ 1 ]  -  mx [  i-1  ]  )
• 解释：要使  i  和  1  的冲突最大，而且还不能让  i  和  i-1  的冲突太大，那就表明  i-1  和  1  的冲突要尽可能的小，而  A[1]  中除去   mx[i-1]   之后，剩下的所有元素都合适，故得证。
• 方程式2：mx[  i  ]=max (  0  ,   a  [  i  ]  --  (  x  -  a  [  i  -  1  ]  -  a  [  1  ]  +  maxn  [  i-1  ]));
• 解释：要想使冲突最小，那就意味着除去不得不冲突的，其他一定不冲突。。。设总共有X种不同的勋章（这个事二分出来的） ，a  [  i  ]  --  (  x  -  a  [  i  -  1  ]  -  a  [  1  ]  +  maxn  [  i-1  ]  )表示在X种中除去必须和  1  还有  i-1  冲突的，由于可能有重复，所以还要加上maxn  [  i-1  ]  （此时可令  1 和  i-1的冲突很大，这样可以保证剩下来的最多。）如果剩下的额不足 A[ i ]  则表示一定会冲突。
• 判断：最后判断一下mx【N】是否为0，如果为0就意味着当前的X是成立的。
• 最后就是代码
• 对于为什么二分要从最大值开始，是因为MX和MAXN都是在满足与前面不冲突的情况下设立的，可以这样理解，任意一个奇数都可以拆成一个偶数+1，我们必须在满足那个偶数的情况下去处理奇数，也就意味着答案一定比那个偶数成立的还要大，一旦比他小，偶数前面的偶数就已经不满足了，也就一定不会满足这个奇数

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>

 using namespace std;

 const int maxn1=;

 int n,m,a[maxn1],sum,maxn[maxn1],mx[maxn1];
 bool pd(int x)
 {
     maxn[]=mx[]=a[];
     for (int i=;i<=n;i++)
      {
          maxn[i]=min(a[]-mx[i-],a[i]);
          mx[i]=max(,a[i]-(x-a[i-]-a[]+maxn[i-]));
      }
     if (!mx[n])
     {
         return true;
     }
     else
     {
         return false;
     }
 }
 int main()
 {
     ios::sync_with_stdio(false);
     cin>>n;
     for (int i=;i<=n;i++)
     {
         cin>>a[i];
         sum+=a[i];
     }
     int l=a[]+a[];
     int r=sum;
     int ans=sum;
     for (int i=;i<=n-;i++)
     {
         l=max(l,a[i]+a[i+]);
     }
     l=max(l,a[]+a[n]);
     while(l<=r)
     {
         int mid=(l+r)>>;
         if (pd(mid))
         {
             ans=min(ans,mid);
             r=mid-;
         }
         else
         {
             l=mid+;
         }
     }
     cout<<ans<<endl;
 }

最后的最后这题有一个什么乱搞的方法，可以去这位大佬的博客里看看（传送门）

反正这句话我看的是真的爽。。。

最后日常水一下，BK201果然还是太神了。。。ZWJdd果然还是太巨了。。。SHYMM还是太牛了。。。。阿基米德的的那啥盆还是太神奇了。。。。。

最后还有其他没水到的大佬，如果有下次讲题的机会一定水到。