算法与数据结构基础 - 字典树(Trie)

Trie基础

Trie字典树又叫前缀树(prefix tree)，用以较快速地进行单词或前缀查询，Trie节点结构如下：

//208. Implement Trie (Prefix Tree)
class TrieNode{
public:
    TrieNode* children[]; //或用链表、map表示子节点
    bool isWord; //标识该节点是否为单词结尾
    TrieNode(){
        memset(children,,sizeof(children));
        isWord=false;
    }
};

插入单词的方法如下：

    void insert(string word) {
        TrieNode* p=root;
        for(auto w:word){
            if(p->children[w-'a']==NULL) p->children[w-'a']=new TrieNode;
            p=p->children[w-'a'];
        }
        p->isWord=true;
    }

假如有单词序列 ["a", "to", "tea", "ted", "ten", "i", "in", "inn"]，则完成插入后有如下结构：

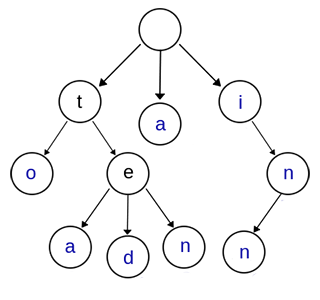
Trie的root节点不包含字符，以上蓝色节点表示isWord标记为true。在建好的Trie结构里查找单词或单词前缀的方法如下：

    /** Returns if the word is in the trie. */
    bool search(string word) {
        TrieNode* p=root;
        for(auto w:word){
            if(p->children[w-'a']==NULL) return false;
            p=p->children[w-'a'];
        }
        return p->isWord;
    }
    /** Returns if there is any word in the trie that starts with the given prefix. */
    bool startsWith(string prefix) {
        TrieNode* p=root;
        for(auto w:prefix){
            if(p->children[w-'a']==NULL) return false;
            p=p->children[w-'a'];
        }
        return true;
    }

相关LeetCode题：

208. Implement Trie (Prefix Tree)  题解

677. Map Sum Pairs  题解

425. Word Squares  题解

1032. Stream of Characters  题解

Trie与Hash table比较

同样用于快速查找，经常会拿Hash table和Trie相互比较。从以上Trie的构建和查找代码可知，构建Trie的时间复杂度和文本长度线性相关、查找时间复杂度和单词长度线性相关；对Trie空间复杂度来说，如果数据按前缀聚拢，那么有利于减少Trie的存储空间。

对Hash table而言，虽然查找过程是O(1)，但另需考虑hash函数本身的时间消耗；另对于字符串prefix查找问题，并不能直接用Hash table解决，要么做一些提前功夫，将各个prefix也提前存入Hash table。

相关LeetCode题：

648. Replace Words  Trie题解  HashTable题解

Trie的应用

Trie除了可以用于字符串检索、前缀匹配外，还可以用于词频统计、字符串排序、搜索自动补全等场景。

相关LeetCode题：

692. Top K Frequent Words

472. Concatenated Words  题解

642. Design Search Autocomplete System  题解