Adaboost原理推导
Adaptive Boosting是一种迭代算法。每轮迭代中会在训练集上产生一个新的学习器,然后使用该学习器对所有样本进行预测,以评估每个样本的重要性(Informative)。换句话来讲就是,算法会为每个样本赋予一个权重,每次用训练好的学习器标注/预测各个样本,如果某个样本点被预测的越正确,则将其权重降低;否则提高样本的权重。权重越高的样本在下一个迭代训练中所占的比重就越大,也就是说越难区分的样本在训练过程中会变得越重要;
先记住这个图:


整个迭代过程直到错误率足够小或者达到一定的迭代次数为止。
分类
首先看一下原来的论文上的伪代码:

Adaboost算法将基分类器的线性组合作为强分类器,同时给分类误差率较小的基本分类器以大的权重值,给分类误差率较大的基分类器以小的权重值;构建的线性组合为:
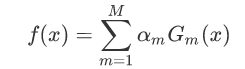
最终分类器是在线性组合的基础上进行Sign函数转换:
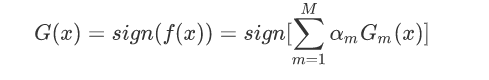
因为G(x)是经过sign化的所以得出的值是-1或1,这时候损失函数自然就是那些被分类错误的样本平均个数了:
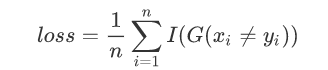
对于这样一个损失函数难以进行求导,所以这里使用下面这个函数代替:
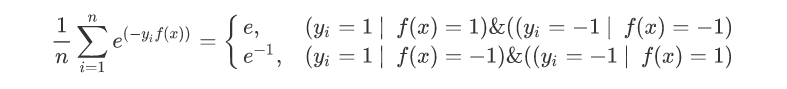
In [1]: import numpy as np
In [2]: np.exp(1)Out[2]: 2.718281828459045
In [3]: 1/np.exp(1)Out[3]: 0.36787944117144233
所以损失函数可以改变为:
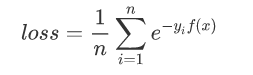
根据刚开始的图示我们可以得出:
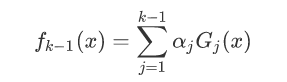
由于这里每个模型都是上一个模型得来的:
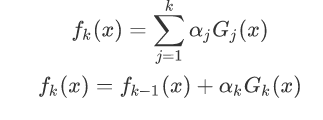
将fk(x)带入到损失函数中:
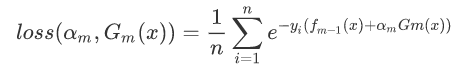
剩下的就是走机器学习的老套路求导求值,这时候就先构造参数:
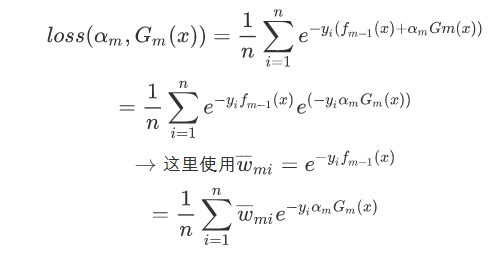
使下列公式达到最小值的αm和Gm就是AdaBoost算法的最终求解值。
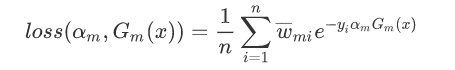
G这个分类器在训练的过程中,是为了让误差率最小,所以可以认为G越小其实就是误差率越小。
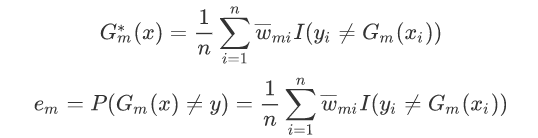
对于αm而言,通过求导然后令导数为零,可以得到公式(log对象可以以e为底也可以以2为底):
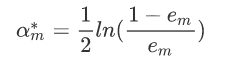
举个栗子
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
x是特征,y是标签,令权值分布
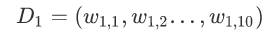
在这里:
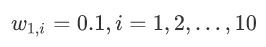
在权值分布为D1的训练数据中,当阀值为2.5的时候,误差率最低,所以这时候的基本分类器为:
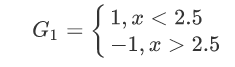
G1(x)在训练数据集上的误差率:

计算模型G1的系数:

更新数据集的权值分布:
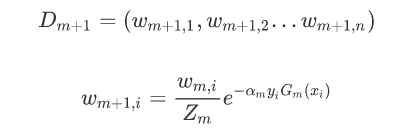
注意这里的Zm是为了归一化:

更新后的结果:
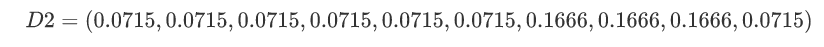
D2中分类正确的样本权值减小,错误分类的样本权值提高。
然后利用D2在训练样本中寻找误差率最低的基本分类器,在继续进行迭代。
......(这里再循环两次)
得到:

所以将新的函数f(x),放入sign()分类器中,从而输出结果:
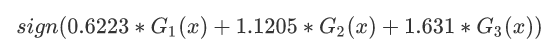
分类器sign(f3(x))在训练数据集上有0个误分类点;结束循环。
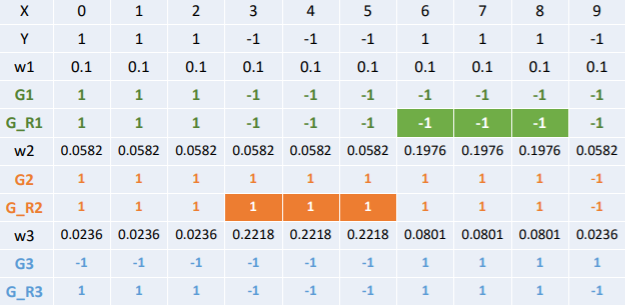

而在实际应用中我们还会添加一个缩减系数:
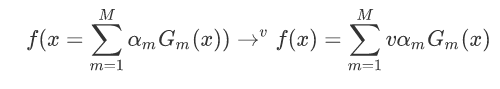
优点:
可以处理连续值和离散值;模型的鲁棒性比较强;解释强,结构简单。
缺点:
对异常样本敏感,异常样本可能会在迭代过程中获得较高的权重值,最终影响模型效果
实现代码:
import pandas as pd
import numpy as np
import math
df = pd.DataFrame([[0,1],[1,1],[2,1],[3,-1],[4,-1],
[5,-1],[6,1],[7,1],[8,1],[9,-1]])
w =np.ones(df.shape[0])/df.shape[0] #初始化权值分布
from sklearn.tree import DecisionTreeClassifier
X = df.iloc[:,[0]]
Y = df.iloc[:,[-1]]
model = DecisionTreeClassifier(max_depth=1).fit(X,Y,sample_weight=w) ##训练第1个模型
model1 = model
# print(w)
# print(w * model.predict(X))
# print(Y.values.T[0])
# print(model.predict(X) != Y.values.T[0])
e = sum(w*(model.predict(X) != Y.values.T[0])) #误差率
# print(e) #0.30000000000000004
a = 1/2*math.log((1-e)/e) #学习器系数
# print(a)
a1 = a
z = sum(w*np.exp(-1*a*Y.values.T[0]*model.predict(X))) #规范因子
w = w/z*np.exp(-1*a*Y.values.T[0]*model.predict(X))#更新权值分布
model = DecisionTreeClassifier(max_depth=1).fit(X,Y,sample_weight=w)##训练第2个模型
model2 = model
e = sum(w*(model.predict(X) != Y.values.T[0]))
a = 1/2*math.log((1-e)/e)
a2 = a
z = sum(w*np.exp(-1*a*Y.values.T[0]*model.predict(X)))
w = w/z*np.exp(-1*a*Y.values.T[0]*model.predict(X))
model = DecisionTreeClassifier(max_depth=1).fit(X,Y,sample_weight=w)##训练第3个模型
model3 = model
e = sum(w*(model.predict(X) != Y.values.T[0]))
a = 1/2*math.log((1-e)/e)
a3 = a
y_ = np.sign(a1*model1.predict(X)+a2*model2.predict(X)+a3*model3.predict(X))##模型组合
print(y_)
最后实在不懂boosting是怎么回事的,就看一下下面的图:
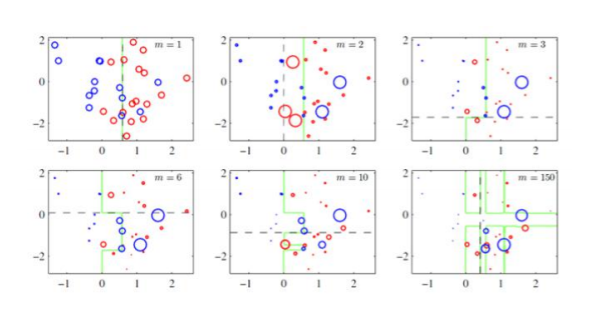
Adaboost原理推导的更多相关文章
- 集成学习之Boosting —— AdaBoost原理
集成学习大致可分为两大类:Bagging和Boosting.Bagging一般使用强学习器,其个体学习器之间不存在强依赖关系,容易并行.Boosting则使用弱分类器,其个体学习器之间存在强依赖关系, ...
- AdaBoost原理详解
写一点自己理解的AdaBoost,然后再贴上面试过程中被问到的相关问题.按照以下目录展开. 当然,也可以去我的博客上看 Boosting提升算法 AdaBoost 原理理解 实例 算法流程 公式推导 ...
- Adaboost原理及目标检测中的应用
Adaboost原理及目标检测中的应用 whowhoha@outlook.com Adaboost原理 Adaboost(AdaptiveBoosting)是一种迭代算法,通过对训练集不断训练弱分类器 ...
- 机器学习之AdaBoost原理与代码实现
AdaBoost原理与代码实现 本文系作者原创,转载请注明出处: https://www.cnblogs.com/further-further-further/p/9642899.html 基本思路 ...
- 机器学习-分类器-Adaboost原理
Adaboost原理 Adaboost(AdaptiveBoosting)是一种迭代算法,通过对训练集不断训练弱分类器,然后把这些弱分类器集合起来,构成强分类器.adaboost算法训练的过程中,初始 ...
- 降维算法----PCA原理推导
1.从几何的角度去理解PCA降维 以平面坐标系为例,点的坐标是怎么来的? 图1 ...
- PCA主成分分析算法的数学原理推导
PCA(Principal Component Analysis)主成分分析法的数学原理推导1.主成分分析法PCA的特点与作用如下:(1)是一种非监督学习的机器学习算法(2)主要用于数据的降维(3)通 ...
- Adaboost原理及相关推导
提升思想 一个概念如果存在一个多项式的学习算法能够学习它,并且正确率很高,那么,这个概率是强可学习的.一个概念如果存在一个多项式的学习算法能够学习它,并且学习的正确率仅比随机猜测略好,那么,这个概念是 ...
- AdaBoost原理,算法实现
前言: 当做重要决定时,大家可能综合考虑多个专家而不是一个人的意见.机器学习处理问题也是如此,这就是元算法背后的思路.元算法是对其他算法进行组合的一种方式,前几天看了一个称作adaboost方法的介绍 ...
随机推荐
- Python:Pandas学习
import pandas as pd import numpy as np s = pd.Series([1, 3, 6, np.nan, 44, 1]) df= pd.DataFrame(np.r ...
- ring3下利用WMI监视进程创建(vc版)
#include "stdafx.h" #define _WIN32_DCOM #include <iostream> using namespace std; #in ...
- U盘免疫
界面如下: 关键部分代码如下: void CImmunityUDlg::OnBnClickedButtonOk() { // TODO: 在此添加控件通知处理程序代码 TCHAR szPath[MAX ...
- Codlility---MinPerimeterRectangle
Task description An integer N is given, representing the area of some rectangle. The area of a recta ...
- 数据管理工具Flux、Redux、Vuex的区别
目录 为什么要进行数据管理? 怎么有效地进行数据管理? 数据管理工具 1. Flux 2. Redux 3. Vuex 使用数据管理工具的场景 相关资料 主要讲解一下前端为什么需要进行数据管理,有效的 ...
- Tido c++线段树知识讲解(转载)
线段树知识讲解 定义.建树.单点修改.区间查询 特别声明:如上的讲解说的是区间最大值 如果想要查询区间和 只需要改变一下建树和查询的代码就行了,如下 其他根据自己的需要进行修改即可
- 移动端使用rem.js,解决rem.js 行内元素占位问题
父级元素: letter-spacing: -0.5em;font-size: 0; 子级元素: letter-spacing: normal; display: inline-block; vert ...
- Metasploit学习笔记
原创博客,转载请注出处! 各位看官可参看——Metasploit实验操作 1.打开msf msfconsole2.帮助选项: msfconsole -h 显示在msf ...
- 查看weblgic/Tuxedo/WebSpere(WAS)/Tomcat中间件版本
1.中间件 1.1 Weblogic WebLogic的版本信息.JDK信息.参数配置均可通过控制台查看. 软件版本 [命令]more /weblogic/bea/logs/log.tx ...
- spring源码深度解析— IOC 之 容器的基本实现
概述 上一篇我们搭建完Spring源码阅读环境,spring源码深度解析—Spring的整体架构和环境搭建 这篇我们开始真正的阅读Spring的源码,分析spring的源码之前我们先来简单回顾下spr ...
