Window10环境下，Stable Diffusion的本地部署与效果展示

Diffusion相关技术最近也是非常火爆，看看招聘信息，岗位名称都由AI算法工程师变成了AIGC算法工程师，本周跟大家分享一些Diffusion算法相关的内容。

Window10环境下，Stable Diffusion的本地部署与效果展示

我选用的版本是：

在Windows下安装部署，只需要：

1. Install Python 3.10.6, checking "Add Python to PATH"
2. Install git.
3. Download the stable-diffusion-webui repository, for example by running git clone https://github.com/AUTOMATIC1111/stable-diffusion-webui.git.
4. Place stable diffusion checkpoint (model.ckpt) in the models/Stable-diffusion directory (see dependencies for where to get it).
5. Run webui-user.bat from Windows Explorer as normal, non-administrator, user.

安装过程中，除了一些包因为网络问题下载不下来，进行了手动下载，还遇到了这个问题

网络问题，可以参考错误处理进行处理。

raise RuntimeError("Cannot add middleware after an application has started")

解决办法是，在powershell中执行下面的命令，重新执行即可：[来自Issues中]

.\venv\Scripts\python.exe -m pip install --upgrade fastapi==0.90.1

正常启动后，在浏览器中输入窗口提示的URL，即可看到下面的画面：

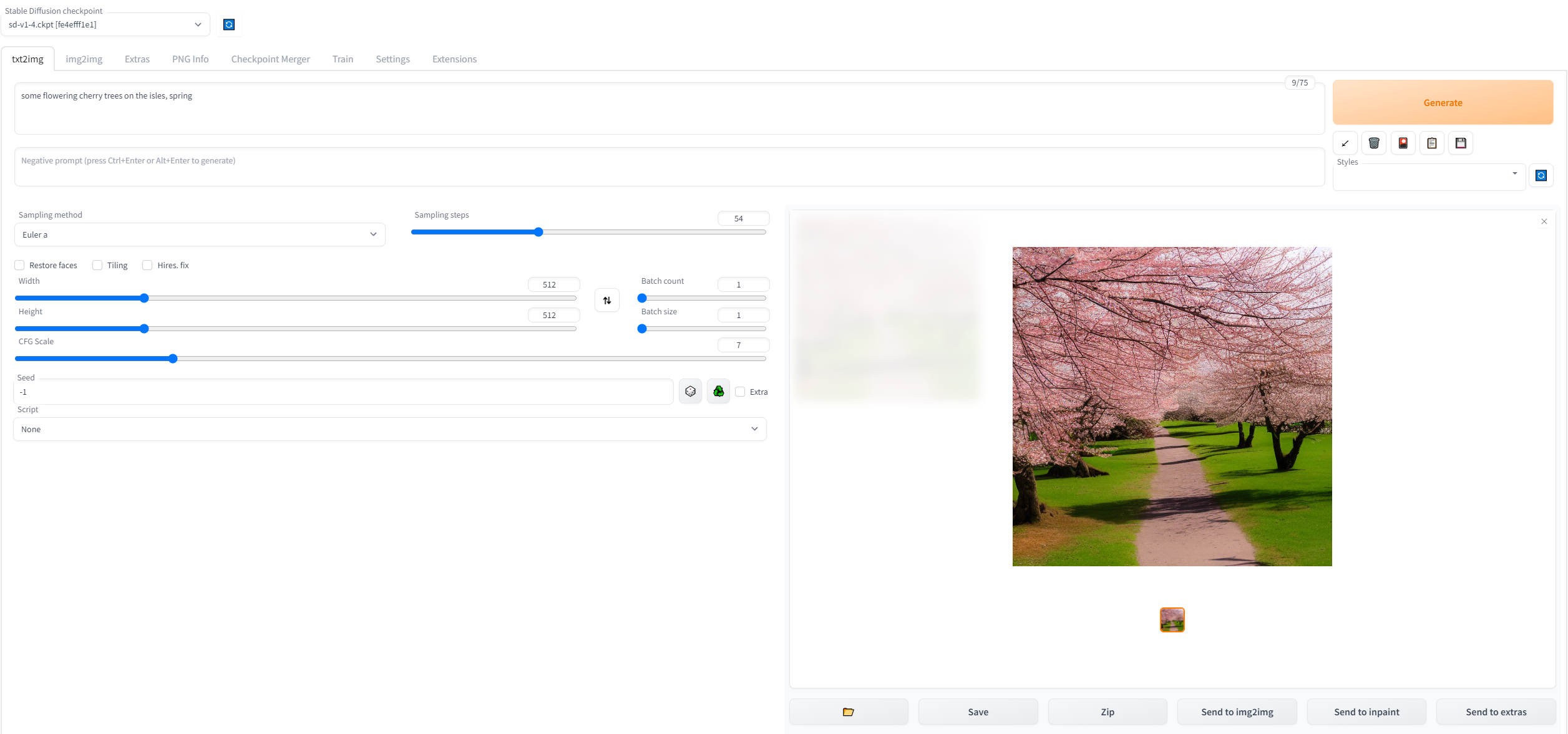
一起来效果吧：

Parametes:

• Step 54
• Sampling method: Euler a
• Width: 512
• Height: 512

Input：some flowering cherry trees on the isles, spring

Input: 草原上一只可爱的小兔子在奔跑，一个萌萌的大眼睛小女孩在追它

他放飞了，生成的东西与想要的完全不搭边儿了。

Input：将上面那句话翻译成英文：A cute little rabbit is running on the grassland, and a cute little girl with big eyes is chasing it

额，感觉它把后半句给丢了，小女孩儿呢？但是，终究兔子是出来了。看来其中的语言模型还是对英文理解更好一些。

下次跟大家分享文章原理，敬请期待。