cost function 成本函数

cost function-成本函数

1、目标

：实现和探索具有一个变量的线性回归的成本函数。

import numpy as np

%matplotlib widget

import matplotlib.pyplot as plt

from lab_utils_uni import plt_intuition, plt_stationary, plt_update_onclick, soup_bowl

plt.style.use('./deeplearning.mplstyle')

我们使用与上一个实验室之前相同的两个数据点；

1000平方英尺的房子以300000美元的价格出售

2000平方英尺的房屋以500000美元的价格出售。

x_train = np.array([1.0, 2.0])           #(size in 1000 square feet)

y_train = np.array([300.0, 500.0])           #(price in 1000s of dollars)

2、计算成本：

变量的成本方程（1）

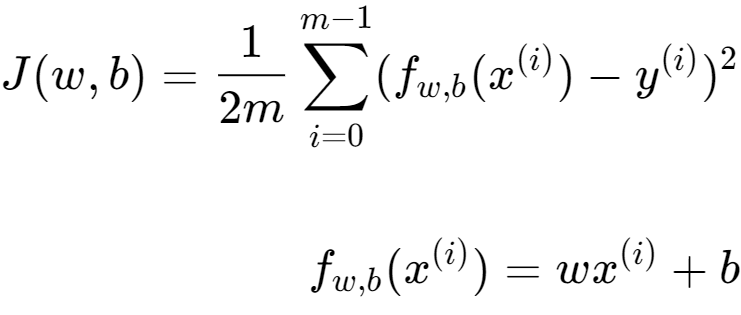
下面是以我们的预测为例，使用参数,（2）

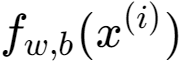
下面是目标值和预测值之间的平方差。（3）

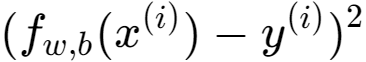
这些差异在所有示例，并除以2m以产生成本，(,)。

注意求和范围通常从 1 到 m，而代码将从 0 到 m-1。

下面的代码通过循环每个示例来计算成本。在每个循环中：

f_wb，计算预测

计算目标和预测之间的差异并平方。

这被添加到总成本中。

def compute_cost(x, y, w, b):

    """

    Computes the cost function for linear regression.

    Args:

      x (ndarray (m,)): 数据，m个示例

      y (ndarray (m,)): 数据，m个示例

      w,b (标量）     : 模型参数

    Returns

        total_cost (float): 使用w，b作为线性回归参数的成本以拟合x和y中的数据点

    """

    # number of training examples

    m = x.shape[0]

    cost_sum = 0

    for i in range(m):

        f_wb = w * x[i] + b

        cost = (f_wb - y[i]) ** 2

        cost_sum = cost_sum + cost

    total_cost = (1 / (2 * m)) * cost_sum

    return total_cost

你的目标是找到一个模型,()=+, 带参数, , 它将在给定输入的情况下准确预测房屋价值。

成本是衡量模型在训练数据上的准确性的指标。

上面的成本方程（1）表明，如果和可以这样选择，使得预测,() 匹配目标数据, (,(())−())2 将为零并且成本最小化。

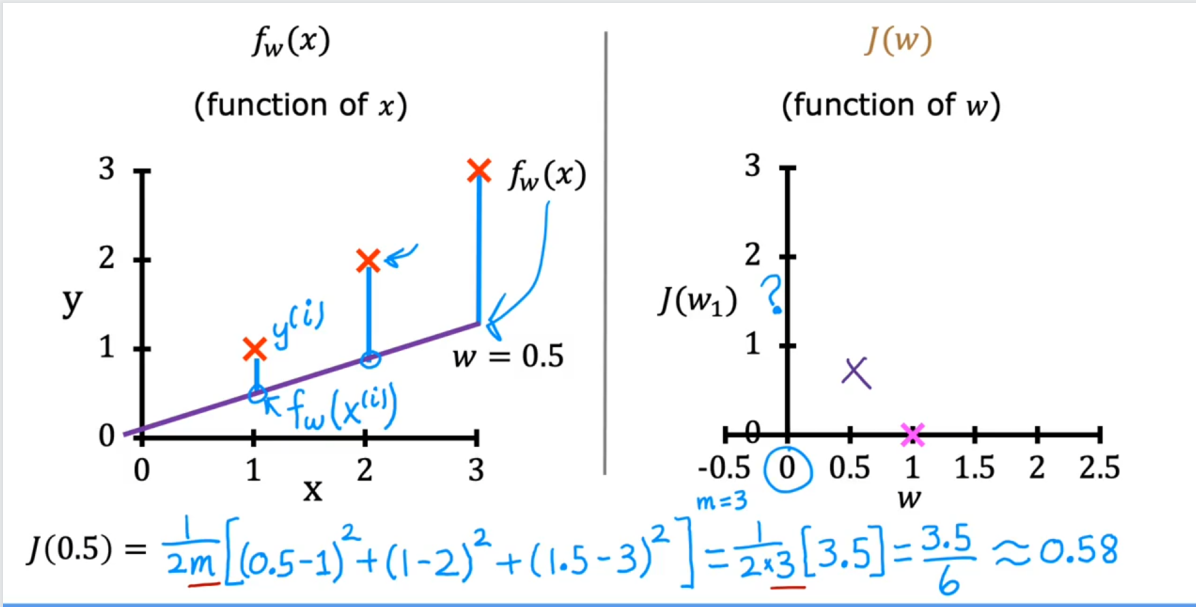
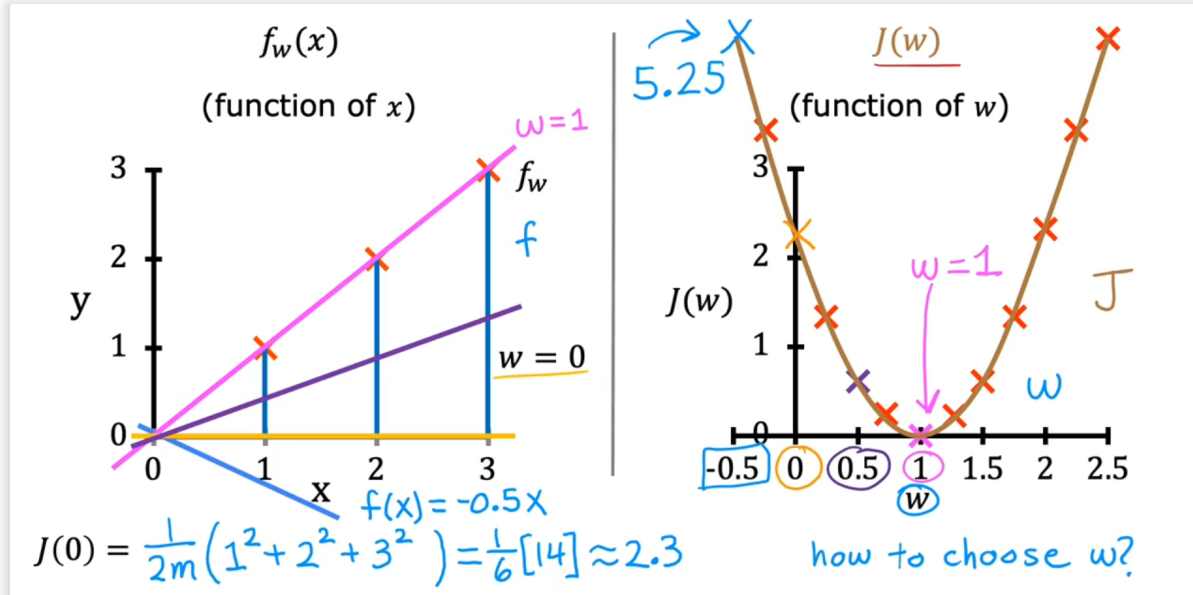
在这个简单的两点示例中，在之前的实验中，确定=100提供了最佳解决方案，所以让我们设置到100，并专注于。

下面，使用滑块控件选择的值从而使成本最小化。

plt_intuition(x_train,y_train)

interactive(children=(IntSlider(value=150, description='w', max=400, step=10), Output()), _dom_classes=('widge…

该图包含一些值得注意的点。当=200，与之前实验室的结果相匹配。

由于目标和修脚之间的差异在成本方程中是平方的。

因此当要么太大，要么太小。

使用通过最小化成本选择的w和b会生成一条与数据完美匹配的线。

3、成本函数可视化-3D

提供了绘图例程，例程位于本地目录的lab_utils_uni.py中。

4、更大的数据集

它使用指导性来查看具有更多数据点的方案。此数据集包括不在同一行上的数据点。这对成本方程式意味着什么？我们能找到吗和那会给我们0的成本？

x_train = np.array([1.0, 1.7, 2.0, 2.5, 3.0, 3.2])

y_train = np.array([250, 300, 480,  430,   630, 730,])

plt.close('all')

fig, ax, dyn_items = plt_stationary(x_train, y_train)

updater = plt_update_onclick(fig, ax, x_train, y_train, dyn_items)

Figure

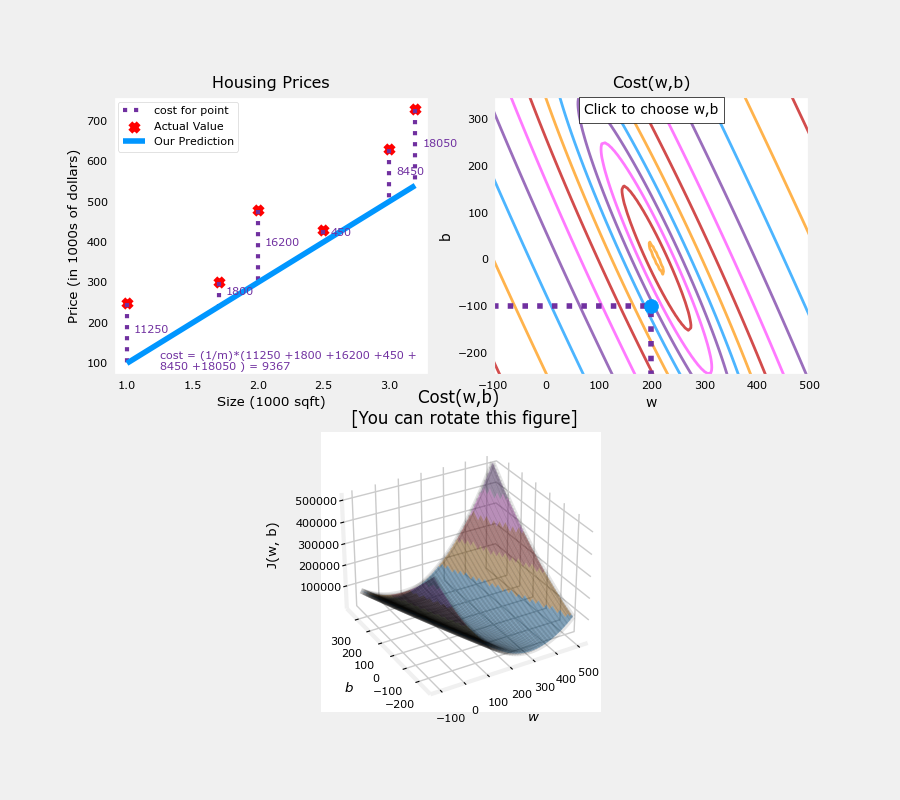
请注意左图中的虚线。这些表示训练集中每个示例贡献的成本部分。在这种情况下，值大约 w=209和 b=2.4提供低成本。请注意，由于我们的训练示例不在一条线上，因此最小成本不为零。

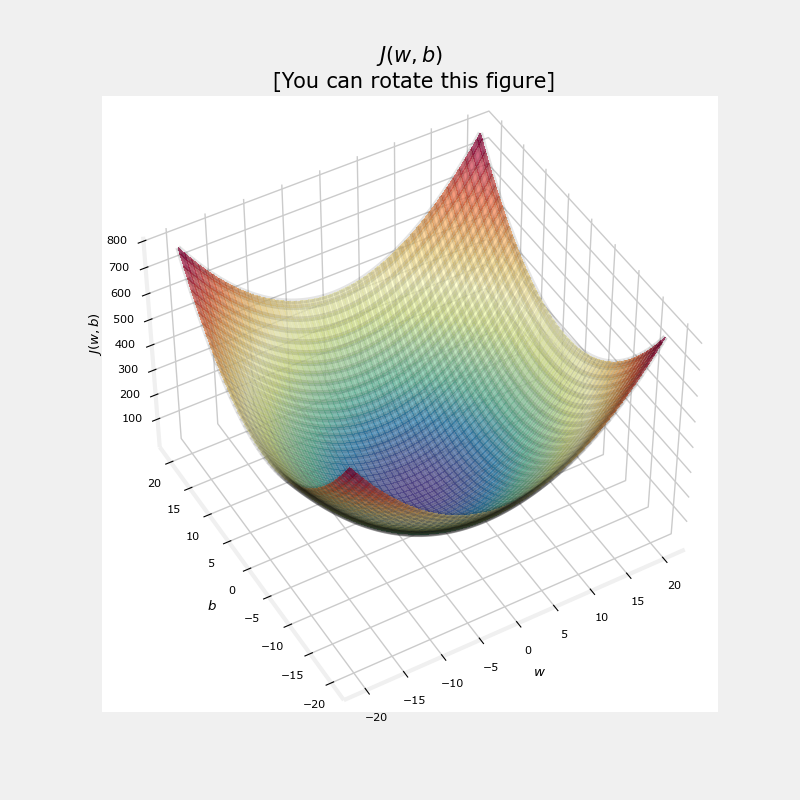
5、凸成本曲面

本函数对损失进行平方的事实确保了“误差面”像汤碗一样凸起。它将始终具有一个最小值，可以通过遵循所有维度的梯度来达到该最小值。在上一个剧情中，因为和尺寸缩放不同，这不容易识别。下图，其中和是对称的。

soup_bowl()

Figure