【LeetCode贪心#09】用最少数量的箭引爆气球（涉及区间重叠情况判断）

用最少数量的箭引爆气球

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以纵坐标并不重要，因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。

一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend，且满足 xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

给你一个数组 points ，其中 points [i] = [xstart,xend] ，返回引爆所有气球所必须射出的最小弓箭数。

示例 1：

输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：对于该样例，x = 6 可以射爆 [2,8],[1,6] 两个气球，以及 x = 11 射爆另外两个气球

示例 2：

输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4

示例 3：

输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2

示例 4：

输入：points = [[1,2]]
输出：1

示例 5：

输入：points = [[2,3],[2,3]]
输出：1

提示：

0 <= points.length <= 10^4
points[i].length == 2
-2^31 <= xstart < xend <= 2^31 - 1

思路

题意理解

题干描述套了一个“打气球”作为背景，搞得有点抽象，其实就是给一个二维数组，寻找里面子数组的重合区间的一个问题

题意图解如下：

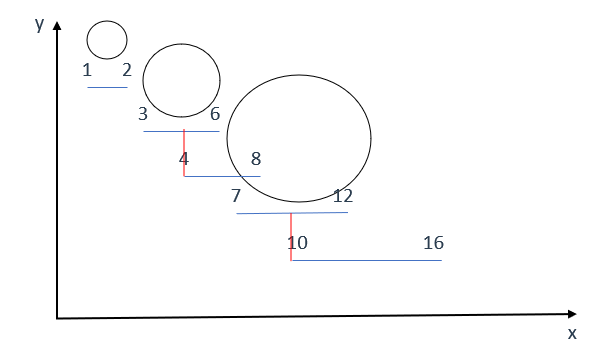
输入：points = [[1,2],[3,6],[4,8],[7,12],[10,16]]
输出：3

如图所示，[1,2]和[3,6]两个区间所代表的的“气球”没有重合，因此不能同时打爆

而[3,6]和[4,8]位置的两个“气球”是有重合的，因此可以使用一支箭同时打爆

同理[7,12]和[10,16]位置也可以消耗一支箭打爆两个气球，因此要打爆所有气球，最少使用的箭数是3

你可能会想：那为什么不能同时打爆[4,8]和[7,12]位置的气球呢？

如果是上面这种打法，那不重叠的[3,6]和[10,16]区间又分别需要消耗两支箭，导致整体使用箭数不是最少

因此同时打爆[4,8]和[7,12]位置的气球不是最优解

由上述讨论可以得出贪心思路：

局部最优：让重叠区间尽可能多的在一块，好一次打完

全局最优：使用最少的箭打完所有气球

本题难点有两个：

1、如何模拟射气球的过程

2、如何记录重叠数组

过程模拟

模拟射气球时，不需要真的去删除被射中的气球数组，只需计数即可

还是以上面的图为例

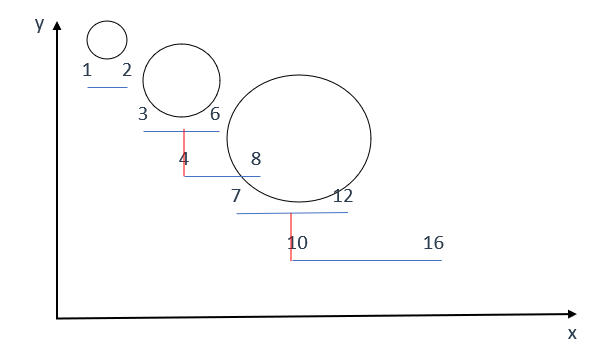
先将所有气球按照左边界排序

情况1：不重叠，需要额外使用箭

以[1,2]和[3,6]为例，[3,6]的左边界3大于[1,2]的右边界2，因此这两个区间无重叠，需要两支箭分别射击，即：

if(points[i][0] > points[i - 1][1]){//左边界3大于右边界2

    res++;//使用弓箭数增加

}

情况2：重叠检查并更新右边界

以[3,6]和[4,8]为例，显然这两个位置的气球时重叠的，那肯定就不满足情况1的条件，因此我们可以接着情况1写在else里面

if(points[i][0] > points[i - 1][1]){//左边界3大于右边界2

    res++;//使用弓箭数增加

}else{//(points[i][0] <= points[i - 1][1]的情况

}

为什么有等于？因为题目说了挨着的气球也可以一次打爆

当气球有重合时，我们不需要使用新的弓箭。但是如果遍历到下一个区间，它也与之前的区间有重合，我们怎么去处理这种情况？

这个时候就需要在遇到重叠区间时，记录当前最小的右边界以提供给下一个区间进行重叠判断

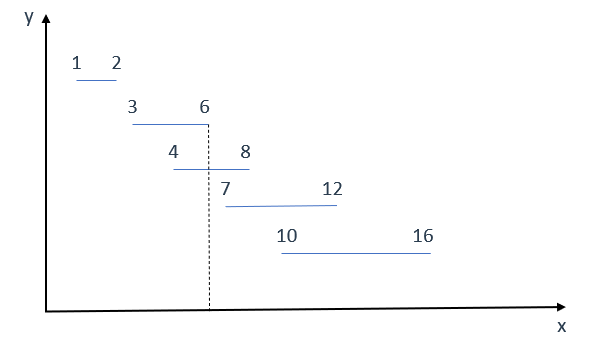
如图所示，当下标i遍历到[4,8]区间时，其与下标为i - 1的[3,6]区间有重合

此时不知道之后会不会还有区间与这两个区间有重合，所以需要记录下这两个区间中最小的那个右边界用于后续判断

最小右边界显然是6，当下标i遍历到[7,12]时，[7,12]的左边界大于当前的最小右边界6

所以[7,12]没有与[3,6]、[4,8]有重叠部分，因此需要额外的弓箭来射击（满足情况1）

所以情况2的代码逻辑如下：

if(points[i][0] > points[i - 1][1]){//左边界3大于右边界2

    res++;//使用弓箭数增加

}else{//(points[i][0] <= points[i - 1][1]的情况

    points[i][1] = min(points[i - 1][1], points[i][1]);//取两个重合区间中最小的右边界作为当前右边界

}

代码

根据上述分析可以总结出以下步骤：

1、自定义比较规则cmp，按左边界对数组先进行排序

2、判断数组为0的情况

2、初始化弓箭数量变量（注意初始值为1，因为0的情况已经判断过，所以之后的情况至少需要一支弓箭）

3、遍历数组，判断两种情况

情况1，无重叠，更新res值记录所需的新弓箭
情况2，有重叠，更新最小右边界，即(points[i] [0] <= points[i - 1] [1]

class Solution {

public:

    static bool cmp(const vector<int>& a, const vector<int>& b){

        return a[0] < b[0];

    }

    int findMinArrowShots(vector<vector<int>>& points) {

        if (points.size() == 0) return 0;//先判断数组为0的情况

        //对二维数组进行排序

        sort(points.begin(), points.end(),cmp);

        int res = 1;//记录弓箭使用数量，因为0的情况已经判断过，所以之后的情况至少需要一支弓箭

        //遍历数组

        for(int i = 1; i < points.size(); ++i){//从1开始，不然比到最后会有负数

            //判断左右边界情况，即重叠情况

            if(points[i][0] > points[i - 1][1]){//情况1，无重叠

                res++;

            }else{//情况2，有重叠，更新最小右边界//(points[i][0] <= points[i - 1][1]

                points[i][1] = min(points[i - 1][1], points[i][1]);

            }

        }

        return res;

    }

};