2022-06-10：薯队长从北向南穿过一片红薯地（南北长M，东西宽N），红薯地被划分为1x1的方格， 他可以从北边的任何一个格子出发，到达南边的任何一个格子， 但每一步只能走到东南、正南、西南方向的

2022-06-10：薯队长从北向南穿过一片红薯地（南北长M，东西宽N），红薯地被划分为1x1的方格，
他可以从北边的任何一个格子出发，到达南边的任何一个格子，
但每一步只能走到东南、正南、西南方向的三个格子之一，
而且不能跨出红薯地，他可以获得经过的格子上的所有红薯，请问他可以获得最多的红薯个数。
来自小红书，小红书第一题。

答案2022-06-10：

动态规划。dp是两行格子。dp[0]是加arr[i][j]之前的最大值数组。dp[1]是加arr[i][j]之后最大值数组。
dp[1][j]=arr[i][j]+max(dp[0][j-1],dp[0][j],dp[[0][j+1])。未来不确定，但是过去是确定的。dp[0]代表过去，dp[1]根据过去的三条方向选择最优方向即可。
时间复杂度：O(MN)。
空间复杂度：O(N)。占用两行格子。

代码用rust编写。代码如下：

fn main() {
    let mut map: Vec<Vec<i32>> = vec![
        vec![3, 5, 6, 2, 4],
        vec![7, 8, 9, 1, 1],
        vec![1, 2, 3, 4, 5],
    ];
    let ans = max_score(&mut map);
    println!("ans = {}", ans);
    let mut map: Vec<Vec<i32>> = vec![
        vec![3, 5, 6, 2, 4],
        vec![7, 8, 9, 1, 1],
        vec![1, 2, 3, 4, 5],
    ];
    let ans = max_score2(&mut map);
    println!("ans = {}", ans);
    let mut map: Vec<Vec<i32>> = vec![
        vec![3, 5, 6, 2, 4],
        vec![7, 8, 9, 1, 1],
        vec![1, 2, 3, 4, 5],
    ];
    let ans = max_score3(&mut map);
    println!("ans = {}", ans);
}

fn max_score(map: &mut Vec<Vec<i32>>) -> i32 {
    let mut ans = 0;
    for col in 0..map[0].len() as i32 {
        ans = get_max(ans, process(map, 0, col));
    }
    return ans;
}

fn process(map: &mut Vec<Vec<i32>>, row: i32, col: i32) -> i32 {
    if col < 0 || col == map[0].len() as i32 {
        return -1;
    }
    if row == map.len() as i32 - 1 {
        return map[row as usize][col as usize];
    }
    let cur = map[row as usize][col as usize];
    let next1 = process(map, row + 1, col - 1);
    let next2 = process(map, row + 1, col);
    let next3 = process(map, row + 1, col + 1);
    return cur + get_max(get_max(next1, next2), next3);
}

fn max_score2(map: &mut Vec<Vec<i32>>) -> i32 {
    let mut ans = 0;
    let n = map.len() as i32;
    let m = map[0].len() as i32;
    let mut dp: Vec<Vec<i32>> = vec![];
    for i in 0..n {
        dp.push(vec![]);
        for _ in 0..m {
            dp[i as usize].push(-2);
        }
    }
    for col in 0..map[0].len() as i32 {
        ans = get_max(ans, process2(map, 0, col, &mut dp));
    }
    return ans;
}

fn process2(map: &mut Vec<Vec<i32>>, row: i32, col: i32, dp: &mut Vec<Vec<i32>>) -> i32 {
    if col < 0 || col == map[0].len() as i32 {
        return -1;
    }
    if dp[row as usize][col as usize] != -2 {
        return dp[row as usize][col as usize];
    }
    // 继续算！
    let mut ans = 0;
    if row == map.len() as i32 - 1 {
        ans = map[row as usize][col as usize];
    } else {
        let cur = map[row as usize][col as usize];
        let next1 = process2(map, row + 1, col - 1, dp);
        let next2 = process2(map, row + 1, col, dp);
        let next3 = process2(map, row + 1, col + 1, dp);
        ans = cur + get_max(get_max(next1, next2), next3);
    }
    dp[row as usize][col as usize] = ans;
    return ans;
}

// 最优方法
fn max_score3(map: &mut Vec<Vec<i32>>) -> i32 {
    let n = map.len() as i32;
    let m = map[0].len() as i32;
    let mut dp: Vec<Vec<i32>> = vec![];
    for _ in 0..2 {
        dp.push(map[0].clone());
    }

    for i in 1..n {
        for j in 0..m as i32 {
            dp[1][j as usize] = get_max(
                get_max(
                    dp[0][j as usize],
                    if j - 1 >= 0 {
                        dp[0][(j - 1) as usize]
                    } else {
                        0
                    },
                ),
                if j + 1 < m {
                    dp[0][(j + 1) as usize]
                } else {
                    0
                },
            ) + map[i as usize][j as usize];
        }
        dp[0] = dp[1].clone();
    }

    let mut ans = dp[0][0];
    for i in 1..m {
        ans = get_max(ans, dp[0][i as usize]);
    }

    return ans;
}

fn get_max<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T {
    if a > b {
        a
    } else {
        b
    }
}

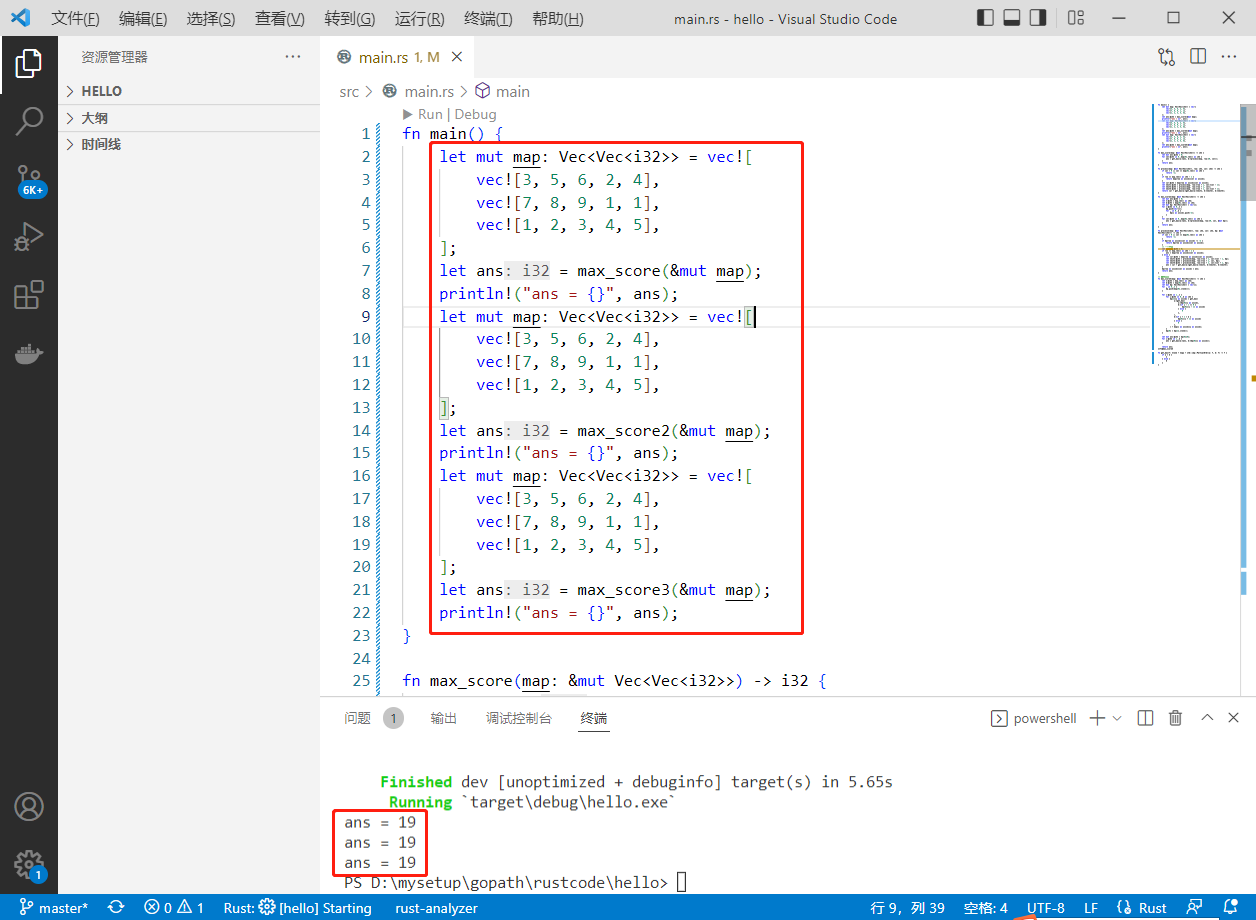
执行结果如下：

---

左神java代码