【Note】贪心

感谢 $ \text{orzws/chy} $ 倾情授课。

目录

• -1. 证明方式
• 0. 朴素贪心
  • AT2557 [ARC073C] Ball Coloring
  • P2587 [ZJOI2008]泡泡堂
• 1. 排序
  • AT2672 [AGC018C] Coins
  • P2123 皇后游戏
    • 严格弱序
  • P1248 加工生产调度
• 2. 数据结构维护相关信息
• 3. 反悔贪心
  • 反悔堆
    • USACO09OPEN 工作调度Work Scheduling
    • CF436E Cardboard Box
    • AT2672 [AGC018C] Coins
  • 反悔自动机
    • CF865D Buy Low Sell High
    • P1792 [国家集训队]种树

贪心与动态规划的一个使用条件是无决策后效性。这个我暂时不大理解，没法写总结

然后就是贪心的一些证明方式。听说很多时候贪心是猜后证明的，然后我可以不证明 对拍试试正确性是么.jpg

-1. 证明方式

1. 微扰：见下 排序贪心；

2. 反证法；

3. 数学归纳法；

4. 局部最优作用范围扩展不会使得整体更劣；

5. 决策包容性：作出局部最优决策后，问题状态空间中的可达集合包含了作出其他任何决策后的可达集合。见下 反悔贪心。

---

0. 朴素贪心

AT2557 [ARC073C] Ball Coloring

所有球中标的最大与最小值一定会被选中，根据此分类讨论。

钦定 \(max\) 取红色，若：

1. \(min\) 取蓝色。那么剩下的贪心，小的给蓝，大的给红。

2. \(min\) 取红色。那么剩下的枚举最小值然后二分最大值，经典求最小极差法。

P2587 [ZJOI2008]泡泡堂

大型田忌赛马（？）

爷的做法：

暴力 \(set\) 日一下（）

优先拿小的去日。

题解做法：

最好的情况是，优先用弱的去赢弱的，打不过就看最强的能不能打过最强的，不行就替补（）

最坏的情况是，把两支队伍反过来就可以了。

---

1. 排序

既然是排序我们就需要关键字。

大致做法是这样的。只考虑相邻两者交换的影响，列不等式求解，得到需要用来排序的关键字。

或者说假设一个最优解，将最优解的邻项交换，看看答案会不会变劣。

（这个叫邻项交换法，也叫微扰？）

AT2672 [AGC018C] Coins

既然有三个选项，不妨缩成两个（）

假设全都选了金币（\(A\)）

设 \(f_i=B_i-A_i\)，\(g_i=C_i-A_i\)

现在就要选 \(y\) 个人选 \(f\) ， \(g\) 个人选 \(g\) 。

考虑 \(i\) ，\(j\) 两者， \(i\) 选 \(f\) ， \(j\) 选 \(g\) 比 \(i\) 选了 \(g\) ， \(j\) 选了 \(f\) 更优，则：

\[f_i+g_j \geq f_j+g_i
\]

即：

\[f_i-g_i \geq f_j-g_j
\]

所以按 \(f-g\) 排个序就好了。

P2123 皇后游戏

浅谈邻项交换排序的应用以及需要注意的问题 By ouuan

忘了先讲国王游戏辽。

皇后游戏中，大臣获得的奖金数目是递增的，我们要使得\(c_n\)尽可能小。

影响\(c_i\)的只有\(c_{i-1}\)，前\(i-1\)个数的顺序并不产生额外影响。前缀子问题最优可推到全局最优。

考虑邻项\(i\)，\(j\)交换。设\(i\)，\(j\)的前一个获得奖金为\(K\)，他们前面所有人的\(a\)值和为\(S\)，则：

1. 当\(i\)在\(j\)之前时：

\[c_i=max\{K,S+a_i\}+b_i
\]

\[c_j=max\{c_i,S+a_i+a_j\}+b_j
\]

1. 当\(j\)在\(i\)之前时：

\[c_j=max\{K,S+a_j\}+b_j
\]

\[c_i=max\{c_j,S+a_j+a_i\}+b_i
\]

当\(i\)在前比\(j\)在前更优：

\(max\{K+b_i+b_j,S+a_i+b_i+b_j,S+a_i+a_j+b_j\}<max\{K+b_i+b_j,S+a_j+b_i+b_j,S+a_i+b_i+a_j\}\)

\(k+b_i+b_j\)那项可以直接去掉了。对于剩下的项，取负再加上\(S+a_i+b_i+a_j+b_j\)，得到：

\[min\{a_j,b_i\}>min\{a_i,b_j\}
\]

经过一系列我看不下去的证明，这个比较是有传递性的。

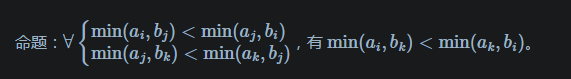
听说直接把这个比较扔进cmp函数也能过。我感觉会\(RE\)（？）

严格弱序

std::sort中比较符必须有的性质，具体如下：

1. 非自反性（自己跟自己比较为false）

2. 非对称性（若x与y比较为true，则y与x比较为false）

3. 传递性（若x与y比较为true，y与z比较为true，则x与z比较为true）

4. 不可比性的传递性（若x与y互相比较为false，y与z互相比较为false，则x与z互相比较为false）

对，他是没有不可比性的传递性的。

优化的话，由于\(a\)的前缀和可能影响全局答案，优先把\(a\)较小的放前面。

证不动正确性了。；w；

P1248 加工生产调度

---

2. 数据结构维护相关信息

---

3. 反悔贪心

贪心的时候，需要注意的是，一定只考虑相邻一步的操作。一些题目确实需要把看起来多样繁琐的操作拆成单位简单操作叠加作用的结果。

仔细思考了一下反悔贪心的原理。一般来说需要一个优先队列，来存储接着某项直接操作/反悔操作的增益

这种贡献是逐步累加的，直到大根堆堆头 $ \leq 0 $ 。

重新百度了一下（（），反悔贪心大致是分为反悔堆和反悔自动机。

反悔堆

通过堆来维护当前贪心策略最优解。

USACO09OPEN 工作调度Work Scheduling

有 $ n $ 项工作，每 $ i $ 项工作有一个截止时间 $ D_i $ ，完成每项工作可以得到利润 $ P_i $ ，求最大可以得到多少利润。

比较基础。按照 $ D_i $ 排序，能做的工作就做，然后以 $ P_i $ 作为关键字放入小根堆。遇到不能做的工作，取出堆顶，如果 $ P_i>top $ 就换掉。

CF436E Cardboard Box

反悔堆的一个常见做法。把可行的各种下一步的策略分别放到不同的堆里面。

比如这道题，从 \(i\) 个星星到 \(i+1\) 个星星就有如下取法：

1. 从未取星星的一关 \(i\) ，获取一个星星，代价 \(a_i\)；

2. 从取了一颗星星的一关 \(i\)，再获取一个星星，代价 \(b_i-a_i\)；

3. 从取了一个星星的一关 \(i\)，把星星扔回去，取另一个未取星星一关 \(j\) 的两个星星，代价 \(b_j-a_i\)；

4. 从取了两个星星的一关 \(i\)，把星星扔回去一个，取另一个未取星星一关 \(j\) 的两个星星，代价 \(b_j-(b_i-a_i)\)。

每次取代价最小一个就行了。

具体的实现细节上，维护的是：

1. 未取星星关的 \(a_i\)（操作1）；

2. 未取星星关的 \(b_i\)（操作3，4）

3. 取一星星关的\(b_i-a_i\)（操作2）；

4. 取一星星关的\(-a_i\)（操作3）；

5. 取两星星关的\(a_i-b_i\)（操作4）。

要把堆中不符合 \(type\) 的数值 \(pop\) 掉。可以看一下这位的实现，写的不错（？）

AT2672 [AGC018C] Coins

重新再看一下这个题。

假设先任意选择。对于三个不同选择的人 \(i\) \(j\) \(k\)，反悔的操作可能有：

1. \(i \longleftrightarrow j\) （\(B_i-A_i+A_j-B_j\)）

2. \(j \longleftrightarrow k\) （\(C_j-B_j+B_k-C_k\)）

3. \(i \longleftrightarrow k\) （\(C_i-A_i+A_k-C_k\)）

4. \(i \longrightarrow j \longrightarrow k \longrightarrow i\) （\(B_i-A_i+C_j-B_j+A_k-C_k\)）

5. \(i \longrightarrow k \longrightarrow j \longrightarrow i\) （\(C_i-A_i+B_k-C_k+A_j-B_j\)）

具体的维护：

1. 选了 \(A\) 的 \(B_i-A_i\)，\(C_i-A_i\)

2. 选了 \(B\) 的 \(A_i-B_i\)，\(C_i-B_i\)

3. 选了 \(C\) 的 \(A_i-C_i\)，\(B_i-C_i\)

反悔自动机

一般是过程中累积贡献，通过差值消去中间项（反悔）来快速得到全局最优解。

CF865D Buy Low Sell High

基本的贪心思路是：买入价格最小的股票，在能赚钱的时候卖出。

当然这个是错的（）

之前也写过一个类似的题目（纪念品/股票市场），由于一天之内价格不会变动，所以可以假装我们先卖了，然后再买进来，之后再卖掉。对于 $ i \leq j \leq k $ ，具体的表现形式是：

$ (p_k-p_j)+(p_j-p_i)=p_k-p_i $

先买入 $ i $ ，再在 $ j $ 卖出，获得 $ p_j-p_i $ 的贡献。然后对于 $ j $ ，接下来有两步可能的操作：

1. 在 $ p_j $ 又买回来，再往后考虑。

2. 在 $ p_j $ 又买回来（相当于在 $ j $ 啥都没干）后，再买 $ p_j $ 。

于是我们可以在队列里面塞两遍 $ p_j $ 。

1. 如果贡献加了一次 $ p_k-p_j $ ，表示 $ j $ 反悔，在 $ i $ 买在 $ k $ 卖；

2. 如果贡献加了一次 $ p_{k_1}-p_j $ ，再加一次 $ p_{k_2}-p_j $ ，表示 $ j $ 先反悔，再 $ j $ 买 $ k_2 $ 卖。

P1792 [国家集训队]种树

反悔自动机，做法是把所有选项扔进堆里，取出堆头 $ b $ ，把与 $ b $ 相邻的两项 \(a\)，\(c\) 合成一个新点 \(a+c-b\)，再扔回堆里面。

看完题解还是纠结了半天两个问题：

1. 这个反悔存储方式是否覆盖了所有可能的下一步

2. 或者未存储的反悔策略不可能成为最优的答案

浅列了一下情况。